Урок геометрии. 11 класс. Тема урока "Применение метода координат к решению задач". Тип урока: урок закрепления, совершенствования знаний и умений. Вид урока: проблемно-исследовательский. Методы: по источнику передачи и восприятия информации (словестные, практические); по степени самостоятельности мышления обучаюихся (репродуктивные, частично-поисковые); по стимулированию интереса к учению(создание ситуации занимательности,ситуации успеха). Формы работы:фронтальная, индивидуальная, коллективная, самостоятельная. Педагогические технологии: по типу познавательной деятельности(обучение по учебникам, использование дополнительной литературы; по подходу к ребенку(личностно-ориентированный, диффреренцированный); по преобладающим методам(развивающее обучение); по направлению(модернизация существующей традиционной системы на основе чередования различных форм и методов работы с обучающимися; по категории обучающихся (технология коллективных способов обучения:индивидуальная, класс-ученик, работа в малых группах).
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
«Применение метода координат к решению задач»
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
««Применение метода координат к решению задач»»
Полезное для учителя
Распродажа видеоуроков!
1390 руб.
1980 руб.
1490 руб.
2130 руб.
1460 руб.
2090 руб.
1680 руб.
2400 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
3560 руб.
17800 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
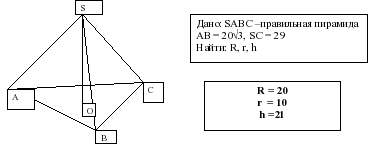
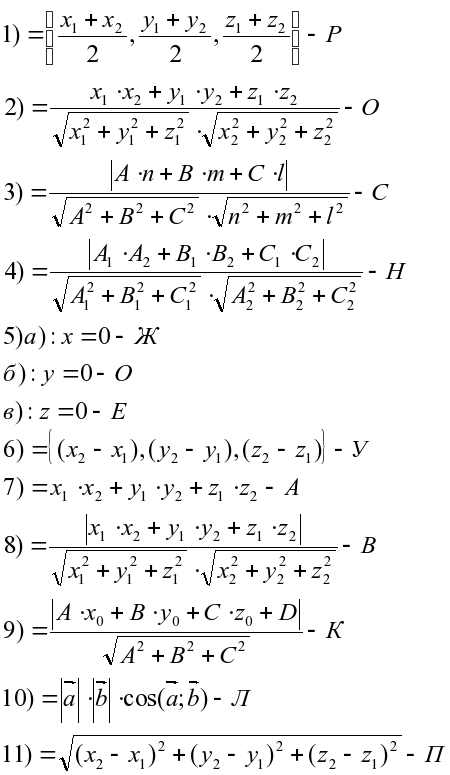

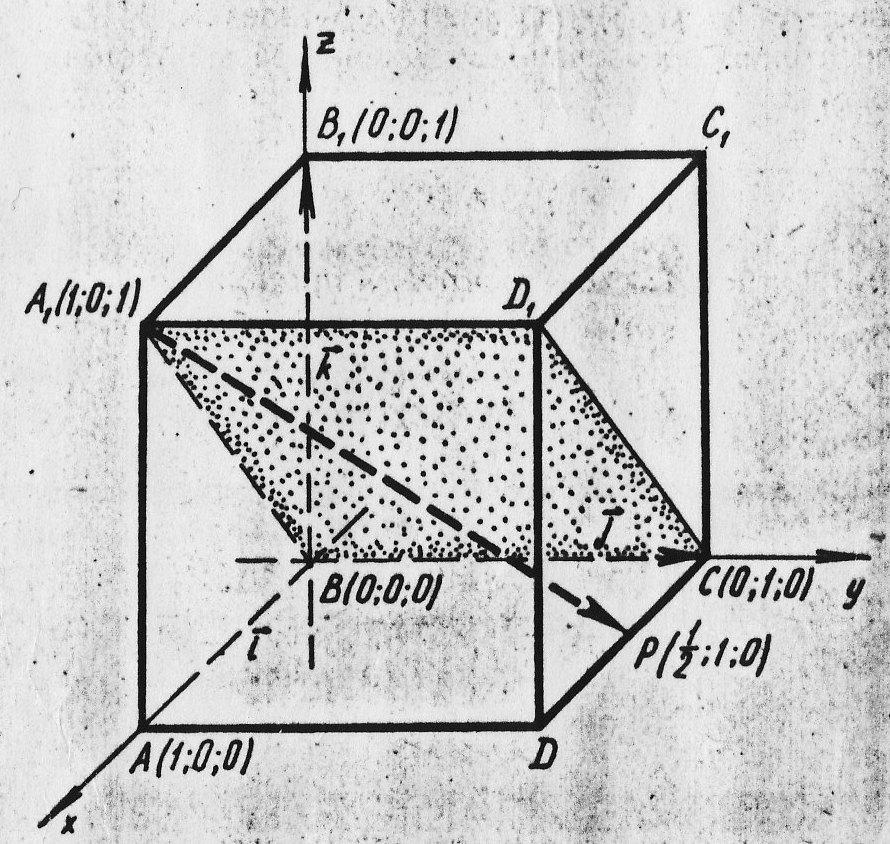 адача № 1
адача № 1



















