Методическая разработка учебного занятия по дисциплине: «Математика» на тему: «Простейшие логарифмические уравнения» составлена для 11класса.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
«Простейшие логарифмические уравнения»
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
««Простейшие логарифмические уравнения»»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1850 руб.
2640 руб.
1650 руб.
2350 руб.
1670 руб.
2380 руб.
1450 руб.
2070 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
2760 руб.
13800 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




 Очень интересной является история возникновения логарифмов. Сообщение: История возникновения логарифма и его применение.
Очень интересной является история возникновения логарифмов. Сообщение: История возникновения логарифма и его применение.  Итак, ребята мы прослушали очень интересные сведения о логарифмах. Ответьте, пожалуйста, на такие вопросы. Что означает термин логарифм? И кто впервые применил его? Объяснение темы. Перед объяснением темы мы посмотрим с вами видео «Математика. Методы решения логарифмических уравнений (1-2)». Ребята, по-вашему, какие уравнения будут называться логарифмическими? (студенты высказывают свои предположения). Определение: уравнения, в которых переменная содержится под знаком логарифма, называют логарифмическими.
Итак, ребята мы прослушали очень интересные сведения о логарифмах. Ответьте, пожалуйста, на такие вопросы. Что означает термин логарифм? И кто впервые применил его? Объяснение темы. Перед объяснением темы мы посмотрим с вами видео «Математика. Методы решения логарифмических уравнений (1-2)». Ребята, по-вашему, какие уравнения будут называться логарифмическими? (студенты высказывают свои предположения). Определение: уравнения, в которых переменная содержится под знаком логарифма, называют логарифмическими.  Сегодня мы изучим несколько методов решения логарифмических уравнений:
Сегодня мы изучим несколько методов решения логарифмических уравнений: 
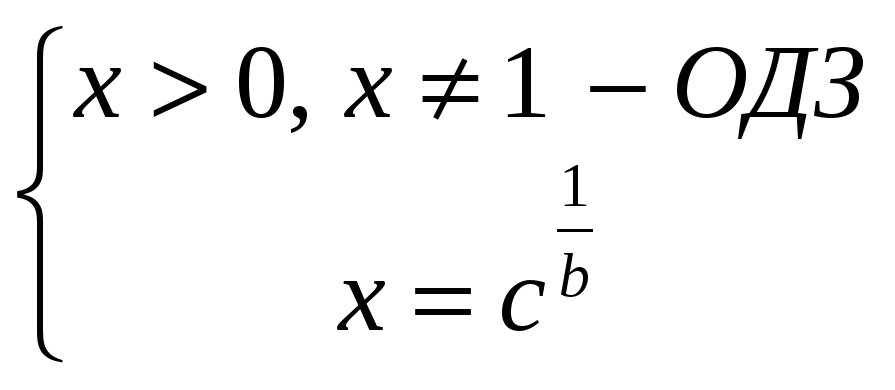 .
.