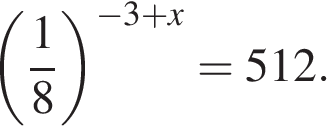Урок введения нового материала. Переход от решения показательных ураввнений к показаателььным нееравенствам.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
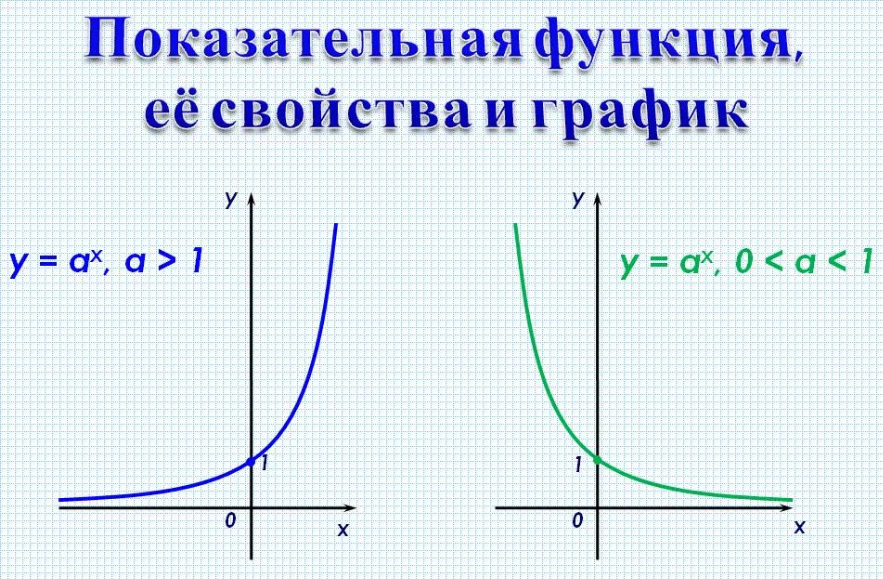
Решение показательных неравенствв
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение показательных неравенствв»
Полезное для учителя
Распродажа видеоуроков!
1490 руб.
2130 руб.
1750 руб.
2500 руб.
1670 руб.
2380 руб.
1670 руб.
2380 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
600 руб.
3000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
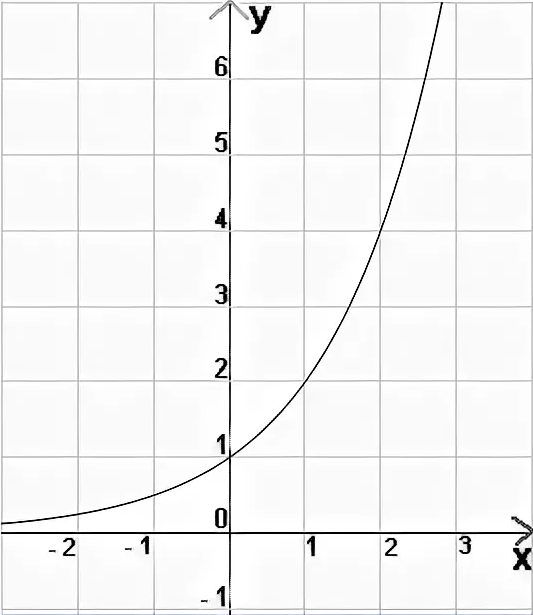
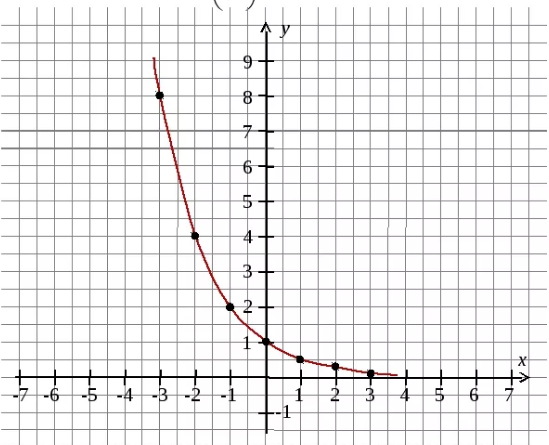 1. Решите графически уравнение : 2х =1/2 2х =4
1. Решите графически уравнение : 2х =1/2 2х =4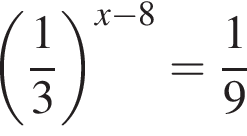 .
.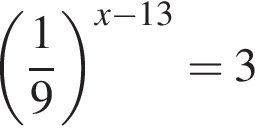 .
.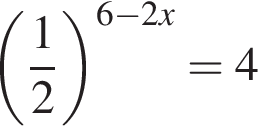 .
.