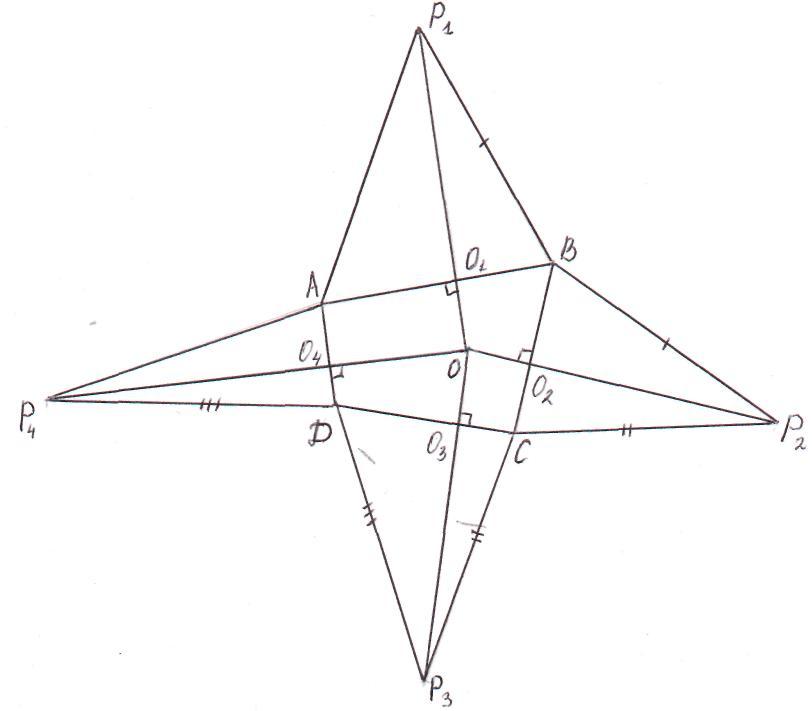
План - конспект урока - соревнования по геометрии в 10 классе (профильный уровень). Тип урока:урок обобщения. На уроке у учащихся формируются навыки конструирования и моделирования, понимание значимости теоретических знаний для решения практических задач. Вырабатывается навык теоретического обоснования всех этапов решения задач. Развивается пространственное мышление детей.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Решение задач с использованием модели пирамиды, план - конспект, 10 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение задач с использованием модели пирамиды, план - конспект, 10 класс »
Полезное для учителя
Распродажа видеоуроков!
1750 руб.
2500 руб.
1490 руб.
2130 руб.
1450 руб.
2070 руб.
1390 руб.
1980 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
3560 руб.
17800 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
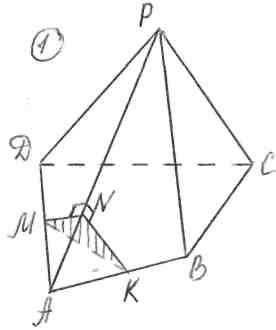 На доске чертежи и решения для трех задач:
На доске чертежи и решения для трех задач: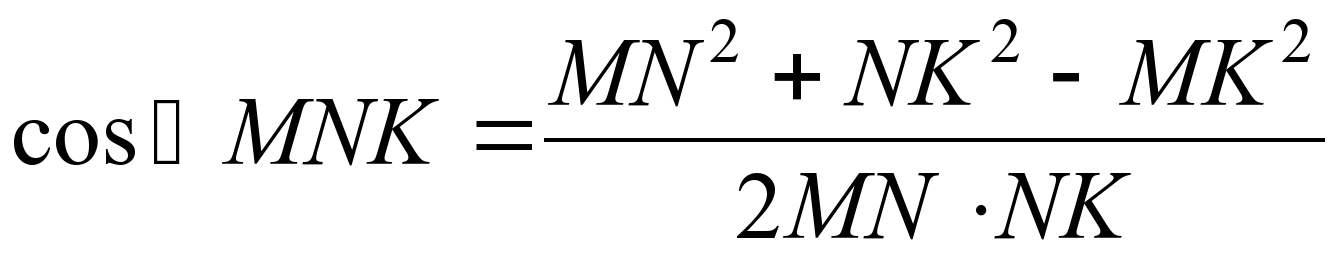 .
. 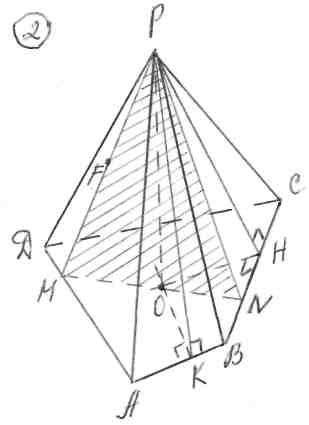 Определение проекции Р на основание.
Определение проекции Р на основание.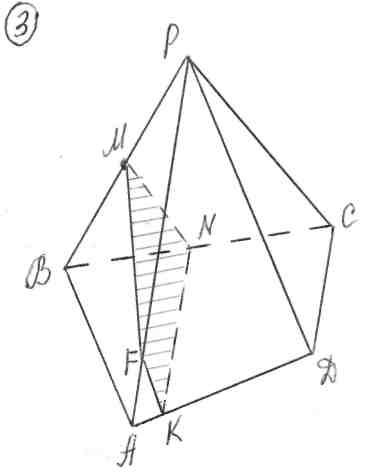 Построение сечения:
Построение сечения: