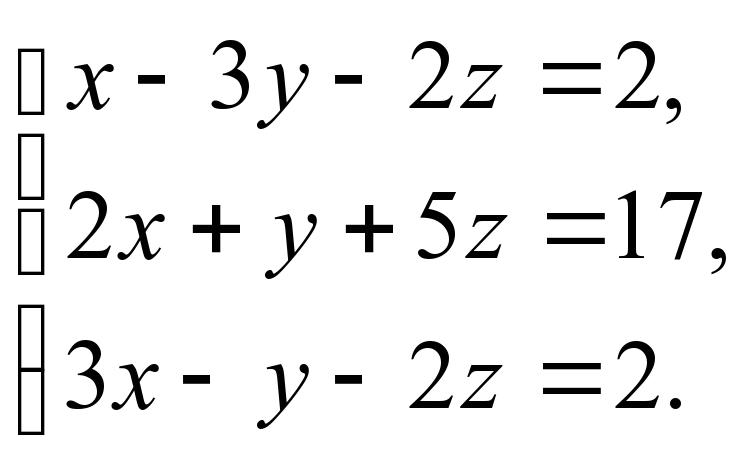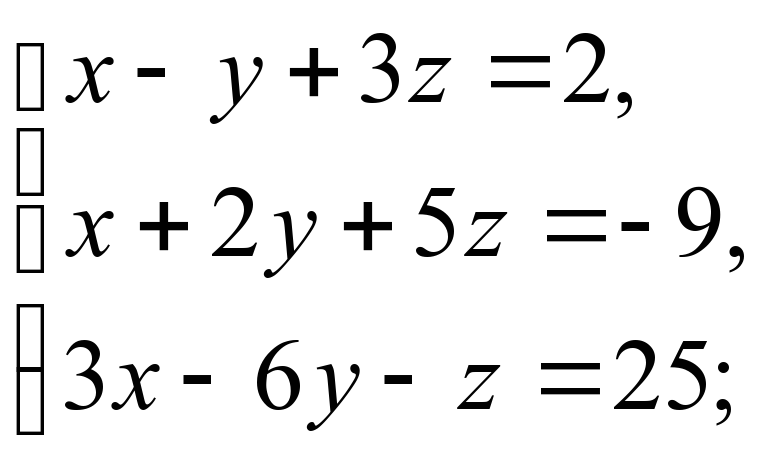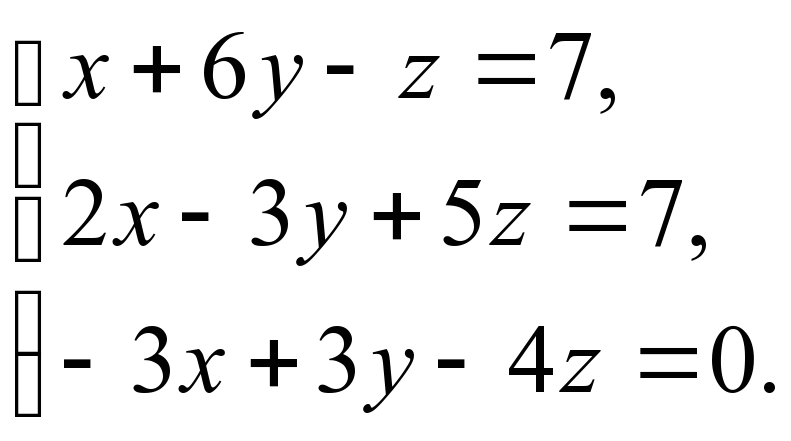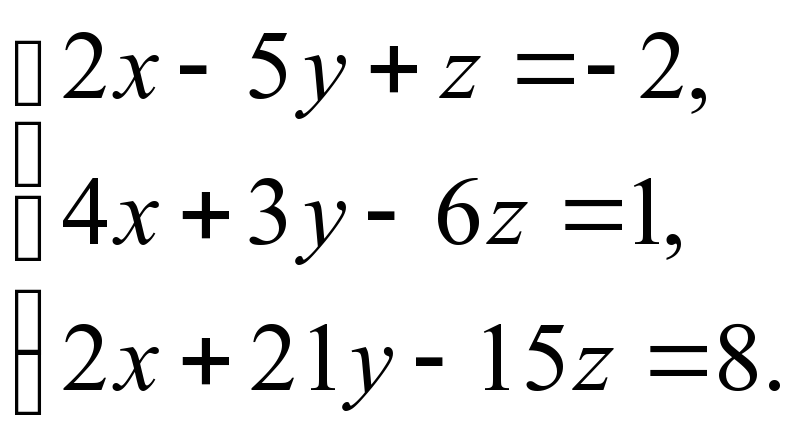ТЕМА: Розв’язування систем лінійних рівнянь за формулами Крамера.
МЕТА: Розширити знання студентів у розв'язуванні систем лінійних рівнянь. Показати застосування правила Крамера при розв'язуванні систем лінійних рівнянь.
Розвивати і удосконалювати обчислювальну культуру студентів, вміння застосовувати наявні в студентів знання в зміненій ситуації, розвивати математичний кругозір, мислення, вміння робити висновки та узагальнення.
Виховувати інтерес до історії математики, уміння планувати свою діяльність.
ТИП: Вивчення нових знань.
ЗАСОБИ НАВЧАННЯ: Персональний комп’ютер, мультимедійний проектор, роздатковий матеріал.
Структура заняття
- Організаційна частина.
- Перевірка домашнього завдання.
- Актуалізація опорних знань.
- Повідомлення теми та мети заняття.
- Мотивація навчальної діяльності.
- Сприймання і усвідомлення матеріалу про розв’язування систем лінійних рівнянь за формулами Крамера.
- Розв’язування вправ.
- Узагальнення та систематизація знань, умінь та навичок студентів.
- Домашнє завдання.
- Підсумок заняття.
Хід заняття
1. Організаційна частина
Викладач з’ясовує присутність студентів на занятті, налаштовує їх на роботу, встановлює психолого – педагогічний контакт з групою.
Викладач роз’яснює зміст роботи на занятті, розповідає про спосіб оцінки знань, умінь та навичок (за окремі види та форми роботи будуть нараховуватись відповідні бали, які студенти будуть самостійно вносити в картки самоконтролю).
2. Перевірка домашнього завдання
Фронтальне опитування (кожна правильна відповідь оцінюється в 0,5б)
Завдання висвітлено на екрані.
1) Визначення матриці.
2) Скільки рядків та стовпців має матриця розміром тхп?
3) Визначення визначника другого та третього порядків.
4) В матриці вкажіть а12 та а21.
5) В матриці знайдіть добуток а12, а21, а33.
6) Які види матриць ви знаєте?
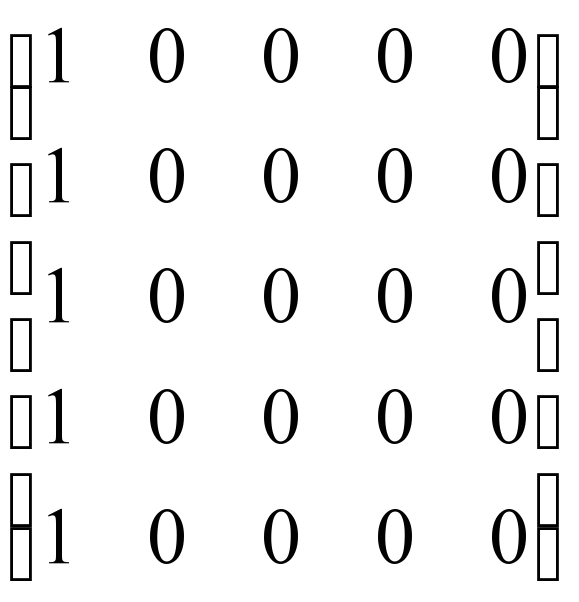
7) Яка з матриць а) одинична; б) нульова; в) діагональна?
1) 2) 3)
4) 5)
8) Формула обчислення визначника другого порядку.
Відповідь: (? = а11а22 – а21а12)
9) Обчисліть визначник . Відповідь: -3.
10) В чому відмінність в запису матриці від детермінанту?
На екрані висвітлено вправи домашнього завдання. Студентам необхідно аргументувати свої кроки обчислення визначників (кожна правильна відповідь оцінюється в 1б)
Обчислити визначники:
3. Актуалізація опорних знань
Фронтальна бесіда (кожна правильна відповідь оцінюється в 0,5б)
1. Які рівняння ми називаємо лінійними?
2. Що таке система лінійних рівнянь з двома невідомими?
3. Які способи розв’язування систем лінійних рівнянь вам відомі?
4. Що взагалі означає розв’язати рівняння, систему рівнянь?
4. Повідомлення теми та мети заняття
Тема заняття: Розв’язування систем лінійних рівнянь за формулами Крамера
Шановні студенти, сьогодні ми з вами попрацюємо над розв’язуванням систем лінійних рівнянь за формулами Крамера. Перед вами стоїть завдання - освоїти цей метод розв’язання рівнянь і показати свої знання та вміння, отримані на попередніх заняттях («Матриці та визначники»).
5. Мотивація пізнавальної діяльності студентів
Сьогодні на занятті ви познайомитеся з одним із методів розв’язання систем лінійних рівнянь за допомогою визначників - з правилом Крамера. Цей метод дуже важливий при вирішенні теоретичних питань, так і при дослідженні систем рівнянь з буквеними коефіцієнтами. Він широко застосовується (як і саме поняття визначника) не тільки у вищій алгебрі, а й в інших розділах вищої математики, механіки та теоретичної фізики. Здобуті вами навички та їх значимість ви оціните при виконанні практичної роботи електротехнічного змісту щодо розрахунку електричного кола постійного струму методом контурних струмів.
Викладач зачитує епіграф до заняття, акцентує увагу студентів на тому моменті, що сьогодні вони познайомляться з формулами Крамера.
Крамер є одним з творців лінійної алгебри. Однією з найбільш відомих його робіт є «Введення в аналіз алгебраїчних кривих», надрукований французькою мовою в 1750 році. В ній Крамер будує систему лінійних рівнянь і вирішує її за допомогою алгоритму, названого пізніше його ім'ям - метод Крамера.
Габріель Крамер народився 31 липня 1704 року в Женеві (Швейцарія) в сім'ї лікаря. Вже в дитинстві він випереджав своїх однолітків в інтелектуальному розвитку і демонстрував неабиякі здібності в області математики.
У 18 років він успішно захистив дисертацію. Через 2 роки Крамер виставив свою кандидатуру на посаду викладача в Женевському університеті. Юнак так сподобався магістрату, що спеціально для нього і ще одного кандидата на місце викладача була створена окрема кафедра математики, де Крамер і працював в наступні роки.
Вчений багато подорожував по Європі, переймаючи досвід у знаменитих математиків свого часу.
Талановитий вчений написав безліч статей на різні теми: геометрія, історія, математика, філософія.
Габріель Крамер помер 4 січня 1752 року у Франції.
6. Сприймання і усвідомлення матеріалу про розв’язування систем лінійних рівнянь за формулами Крамера
Системою лінійних рівнянь з n невідомими називається система
,де а11, …, аmn – дійсні числа, які називаються коефіцієнтами ситеми; х1, …, хn – невідомі; b1, …, bm – дійсні числа, які називаються вільними членами.
Системою лінійних рівнянь з трьома невідомими називається система
,де а11, а12, …, а33 – дійсні числа, які називаються коефіцієнтами ситеми;
х, y, z – невідомі; b1, b2, b3 – дійсні числа, які називаються вільними членами.
Система лінійних рівнянь називається сумісною і визначеною, якщо вона має єдиний розв’язок.
Система лінійних рівнянь називається сумісною, але невизначеною, якщо вона має безліч розв’язків.
Система лінійних рівнянь називається несумісною, якщо вона не має жодного розв’язку.
Нехай задано систему лінійних рівнянь з трьома невідомими
, визначник якої
, то система має єдиний розв’язок
де визначники утворюється із визначника D заміною 1, 2, 3-го стовпців стовпцем вільних членів.
Формули (1) називаються формулами Крамера.
Можливі випадки:
- Якщо D ¹ 0, то система сумісна і визначена, тобто має єдиний розв’язок.
- Якщо D = D1 = D2 = D3 = 0, то система сумісна, але невизначена, отже має безліч розв’язків.
- Якщо D = 0, а хоча б один з допоміжних визначників не дорівнює нулю, то система несумісна – не має жодного розв’язку.
Приклад. Розв’язати слр за допомогою формул Крамера
Розв’язання:
Відповідь: (1; –1; 2)
7. Розв’язування вправ
Розв’язати слр за формулами Крамера: (за правильну відповідь - 1б)
1)
2)
3)
4)
8. Узагальнення та систематизація знань, умінь та навичок студентів
Студенти виконують самостійну роботу за варіантами, висвітленими на слайді (2 варіанти). Після виконання студенти виконують взаємоперевірку за розв’язком, виведеним на екрані. Оцінку вносять в картку контролю.
Варіант 1
Розв’язати слр за формулами Крамера:
Варіант 2
Розв’язати слр за формулами Крамера:
Відповіді
Варіант № 1
(1, 3, -2)
Варіант № 2
(-1, 3, -2)
9. Домашнє завдання
Розв’язати слр за формулами Крамера
1)
2)
3) (не має розв’язку)
4) (безліч розв’язків)
10. Підсумок заняття
Пропонуються питання до аудиторії:
- Що називається системою 3 лінійних алгебраїчних рівнянь з 3 невідомими?
- Що взагалі означає розв’язати систему?
- Написати формули Крамера. Чи завжди за їх допомогою можна розв’язати слр?
Визначники - метод дуже формальний, механічний, користуючись їм думати майже не треба. Добре це чи погано? Звичайно, добре, якщо вам потрібно дуже швидко і дуже багато однотипних систем рівнянь.
При розв'язуванні систем лінійних рівнянь більш високого порядку правило Крамера не завжди доречно, коли необхідно розв’язати систему лінійних рівнянь, в якій число рівнянь не збігається з числом невідомих, тут вже доводиться знаходити n+1 визначників n-го порядку, тому необхідні інші методи розв’язування систем, так наприклад, метод Гаусса. Він застосовується в тому випадку, коли число рівнянь не збігається з числом невідомих і полягає він у послідовному виключенні змінних. Але з цим методом ми познайомимося на наступному занятті.
Потрібно відмітити тих студентів, які отримали більшу кількість балів.
 ІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
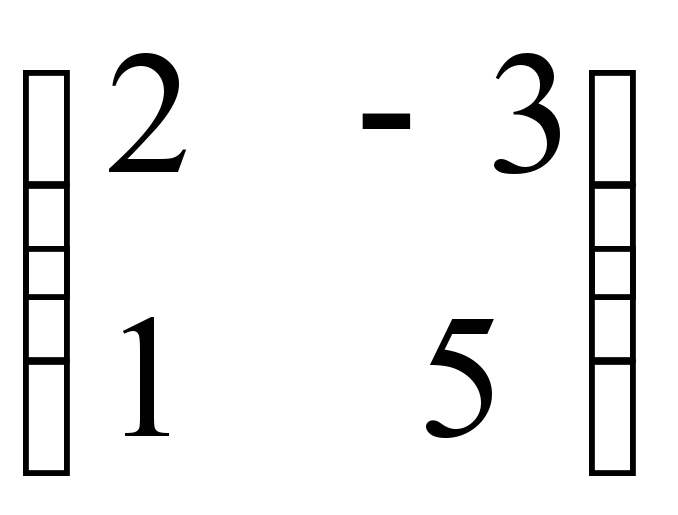 вкажіть а12 та а21.
вкажіть а12 та а21.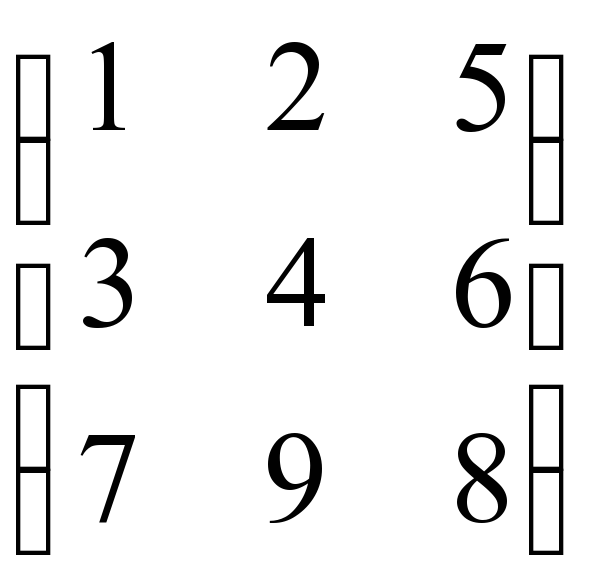 знайдіть добуток а12, а21, а33.
знайдіть добуток а12, а21, а33.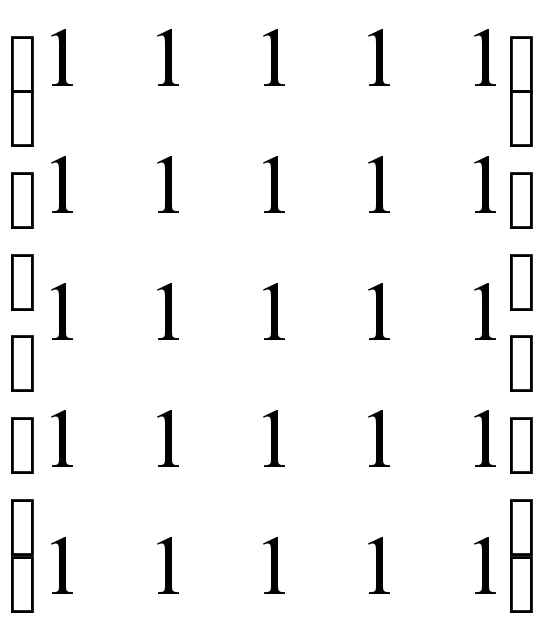 2)
2)  3)
3) 
 5)
5) 
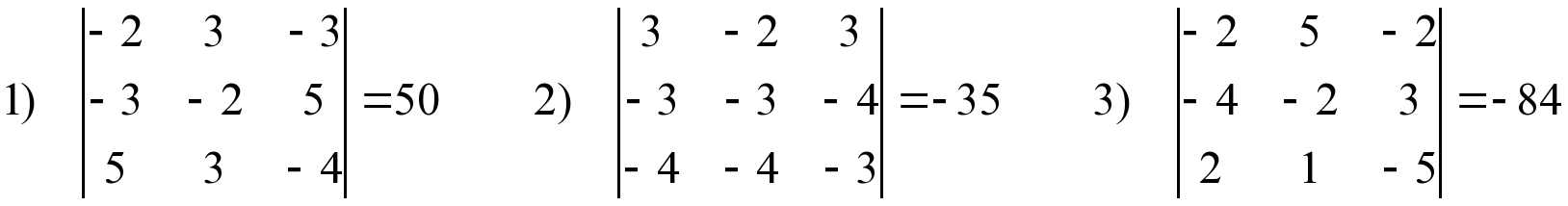
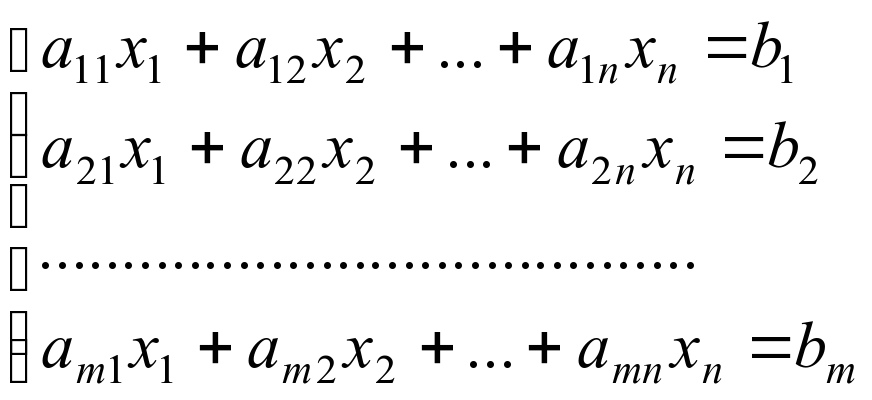 ,
,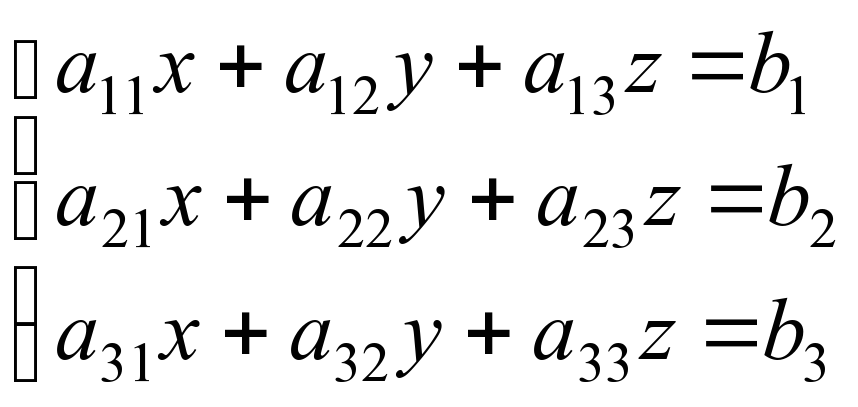 ,
,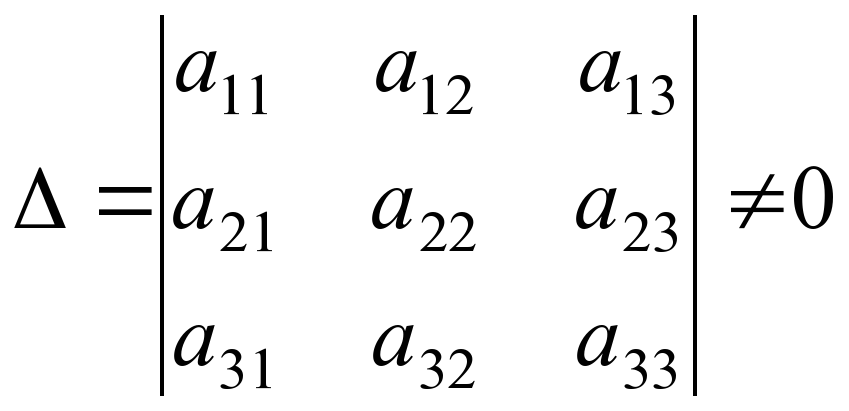 , то система має єдиний розв’язок
, то система має єдиний розв’язок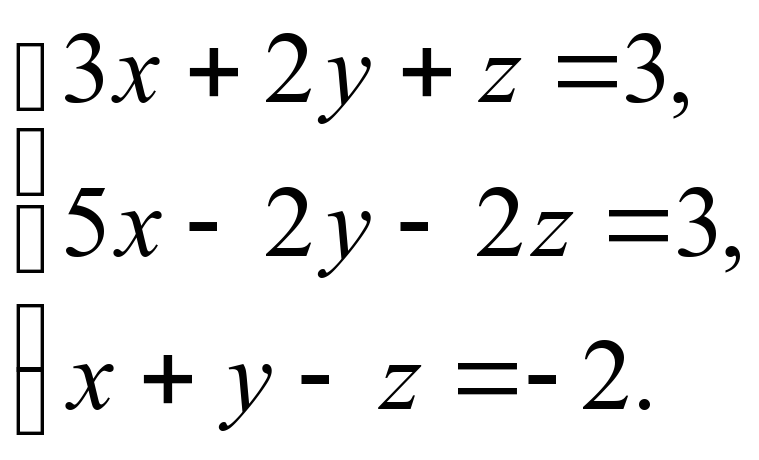
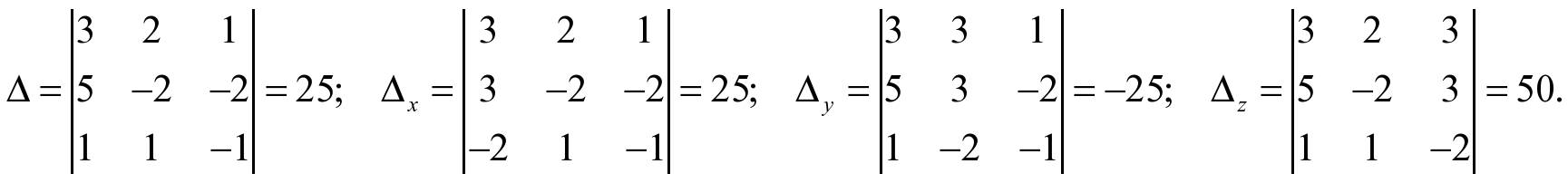


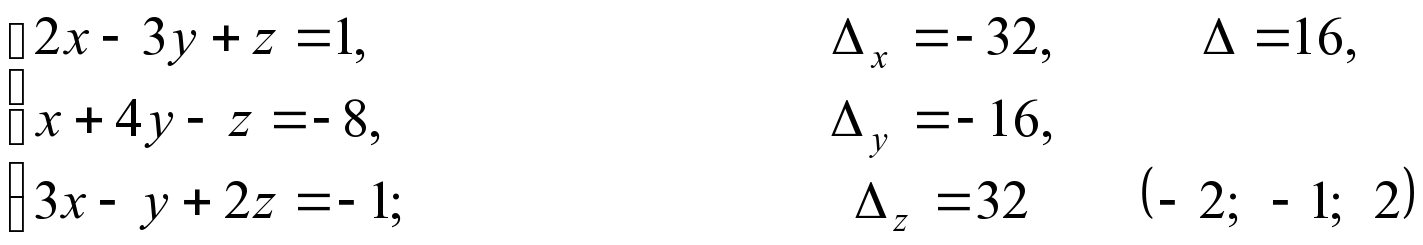

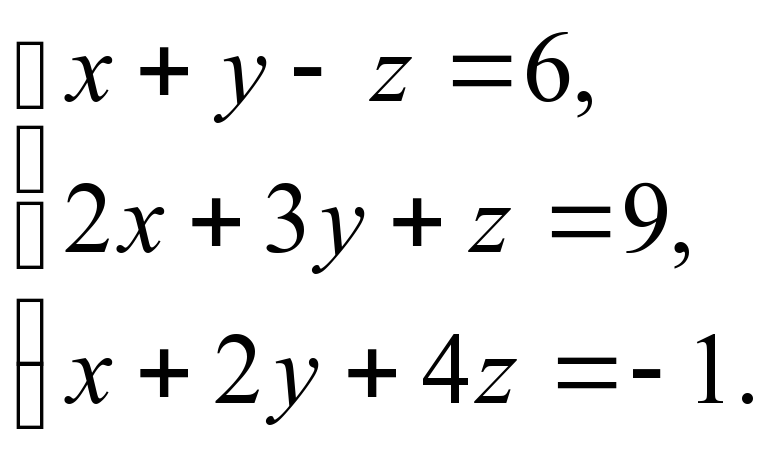
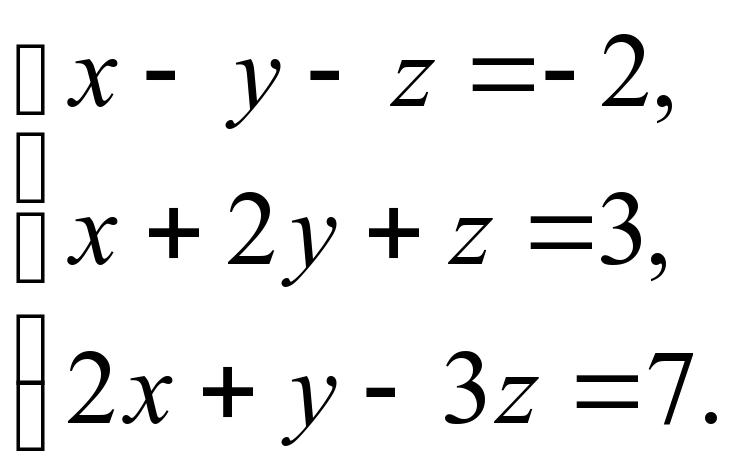
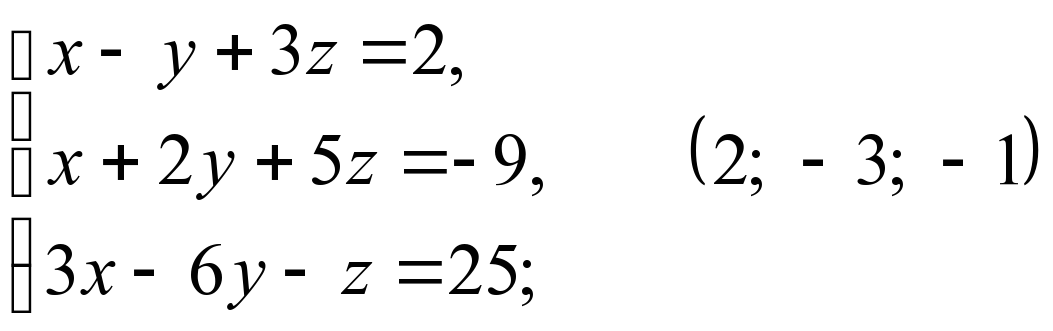
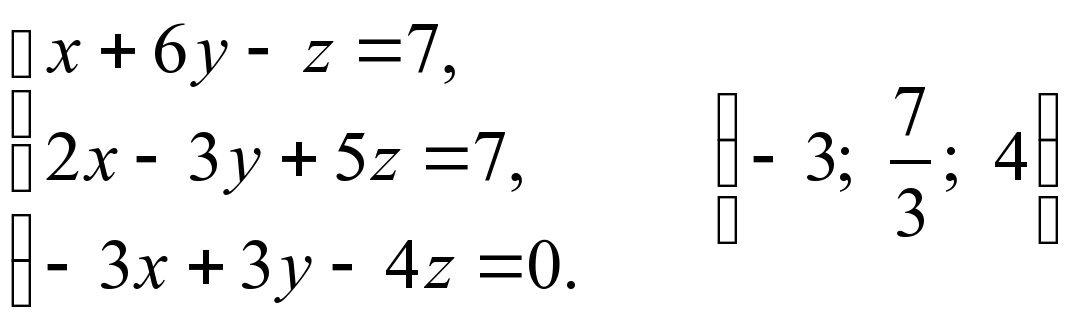
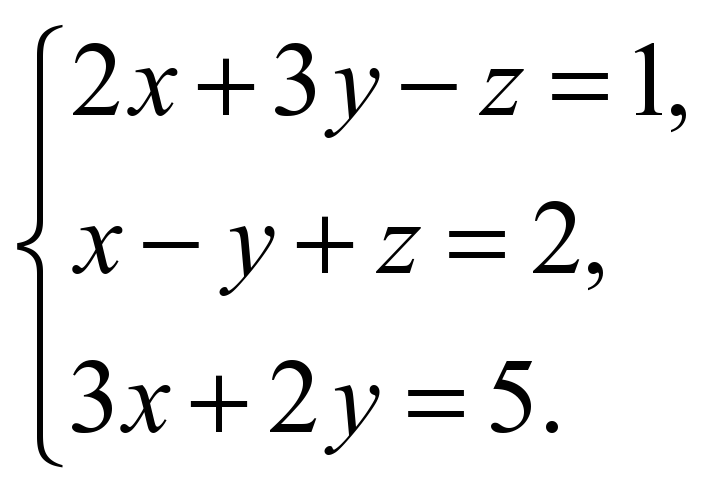 (не має розв’язку)
(не має розв’язку)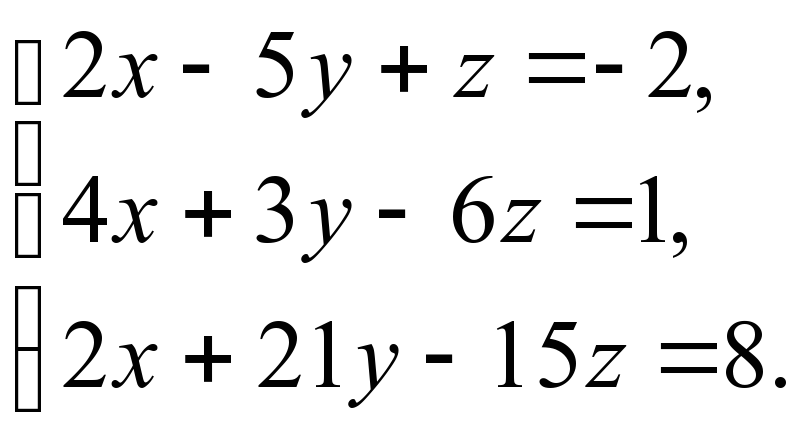 (безліч розв’язків)
(безліч розв’язків)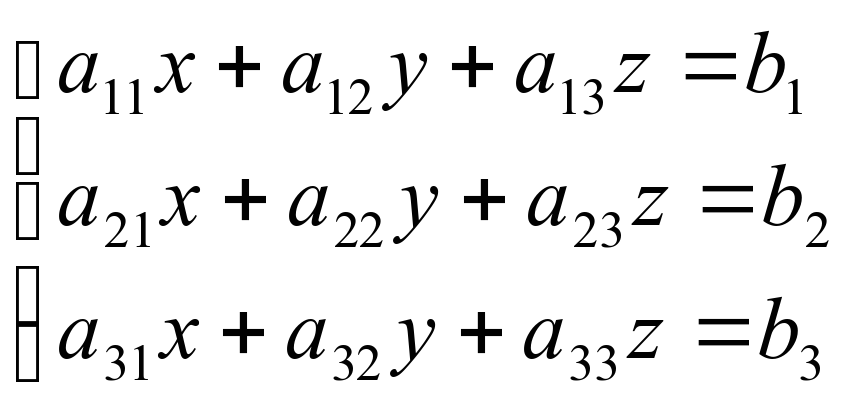 ,
,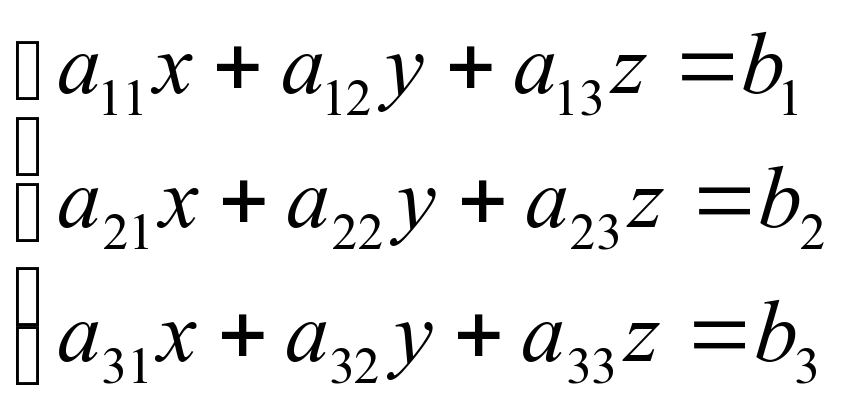 , визначник якої
, визначник якої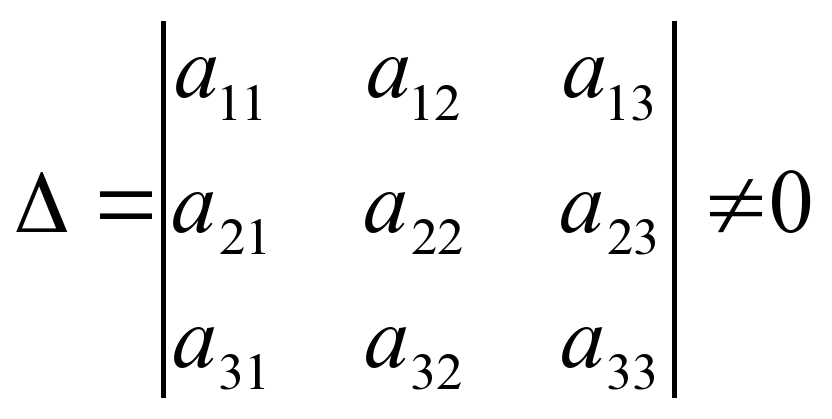 , то система має єдиний розв’язок
, то система має єдиний розв’язок
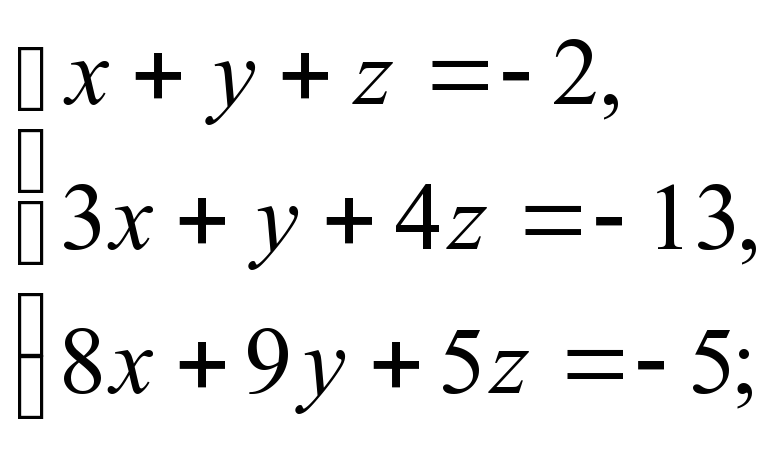 2)
2) 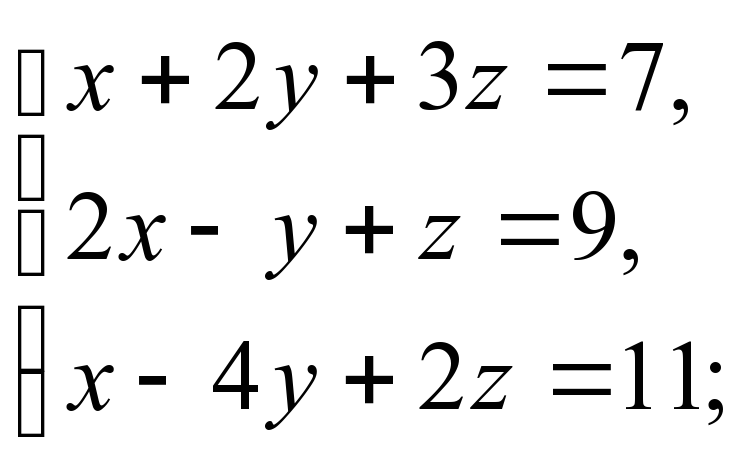 3)
3) 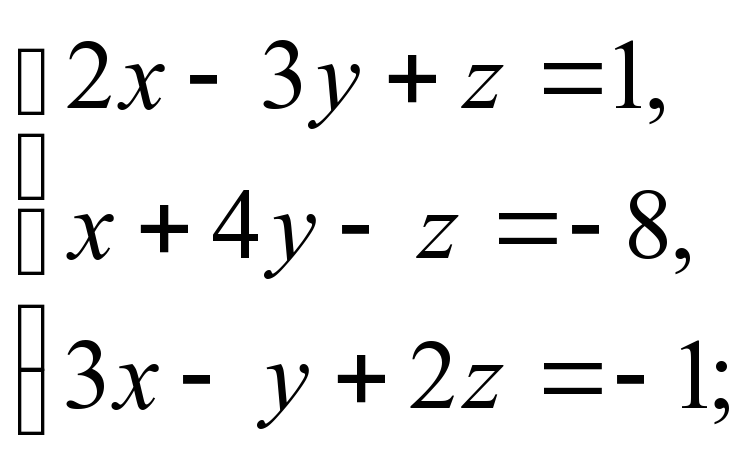 4)
4)