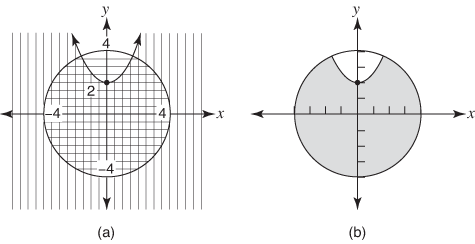
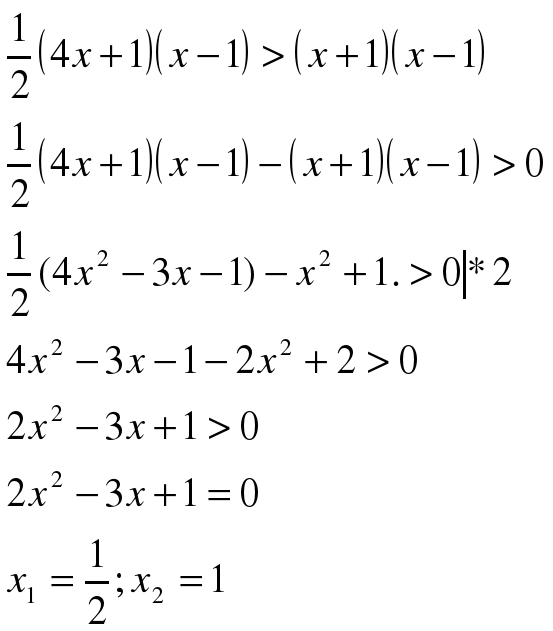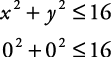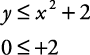данный урок представляет собой разработку урока алгебры на английском языке. можно применять в полиязычком образовании
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
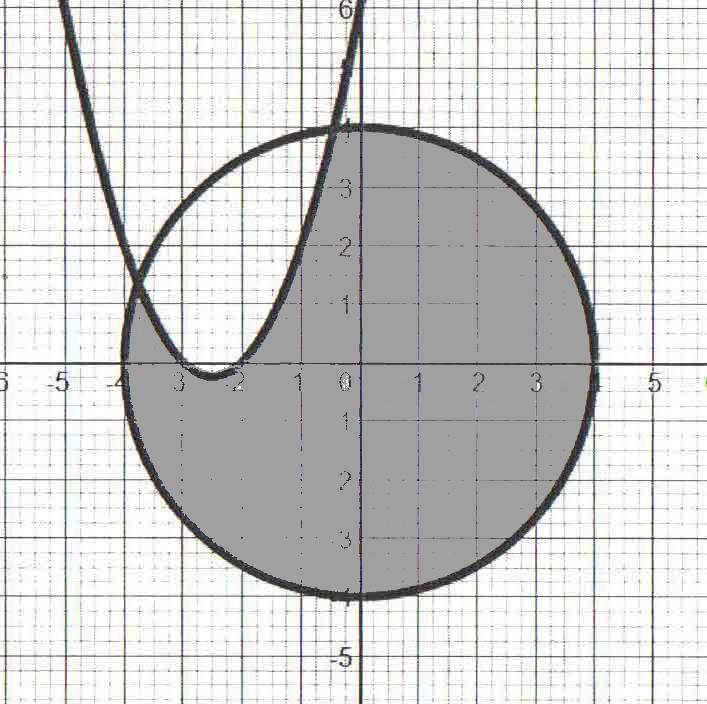
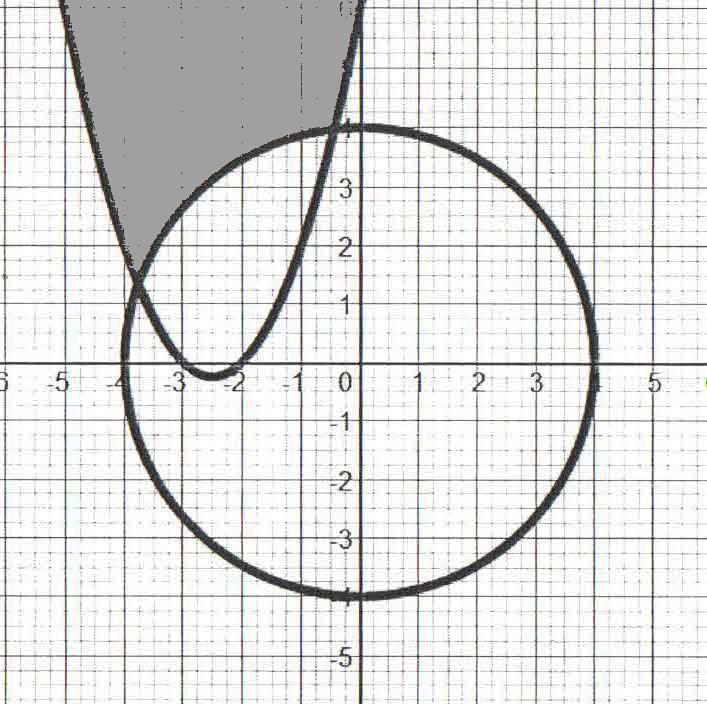
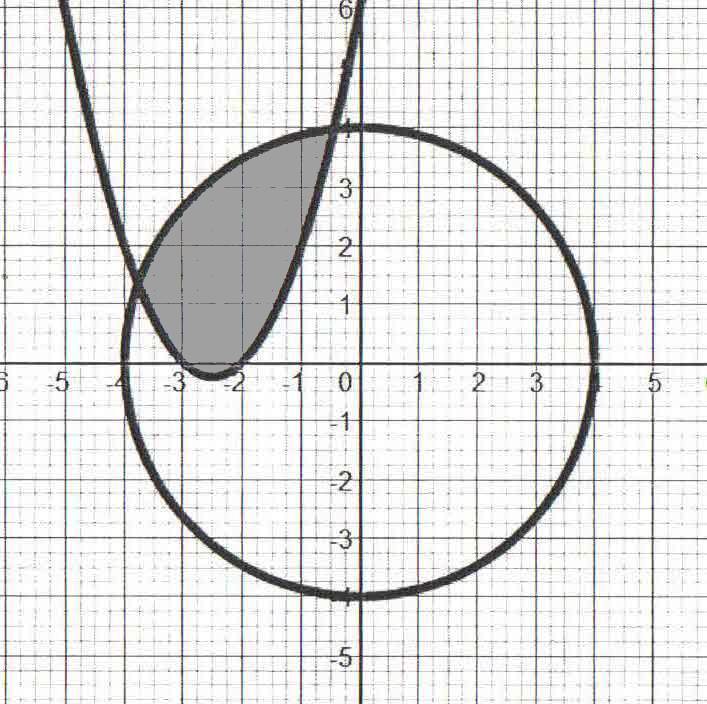
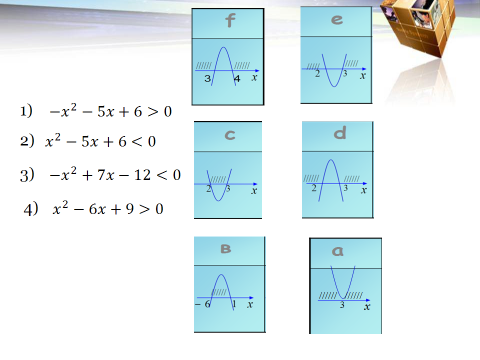
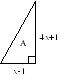
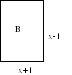
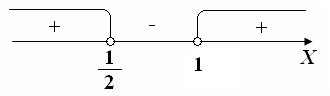
The quadratic inequalities
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«The quadratic inequalities»
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2380 руб.
1670 руб.
2380 руб.
1580 руб.
2260 руб.
1650 руб.
2350 руб.
Курсы ПК и ППК для учителей!
600 руб.
3000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
3560 руб.
17800 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

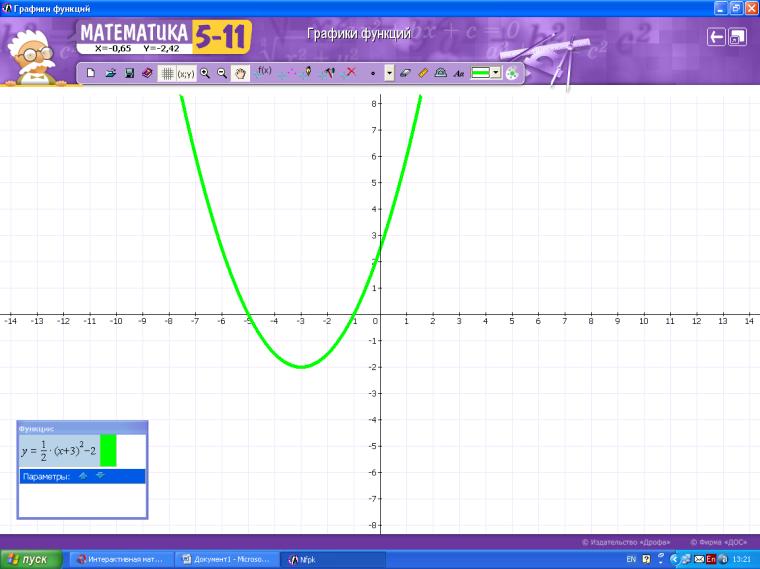
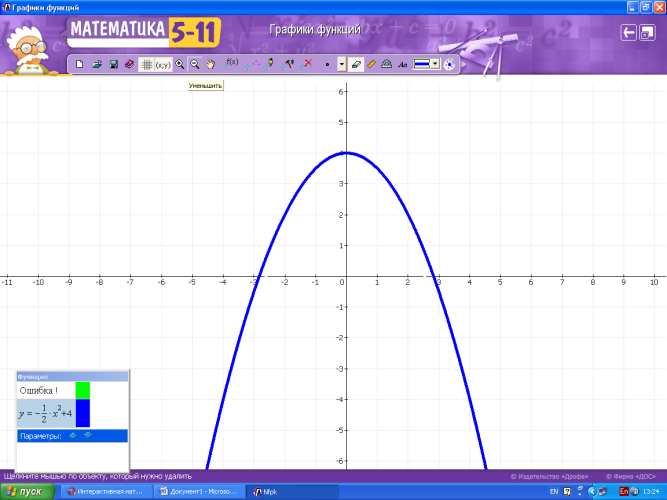
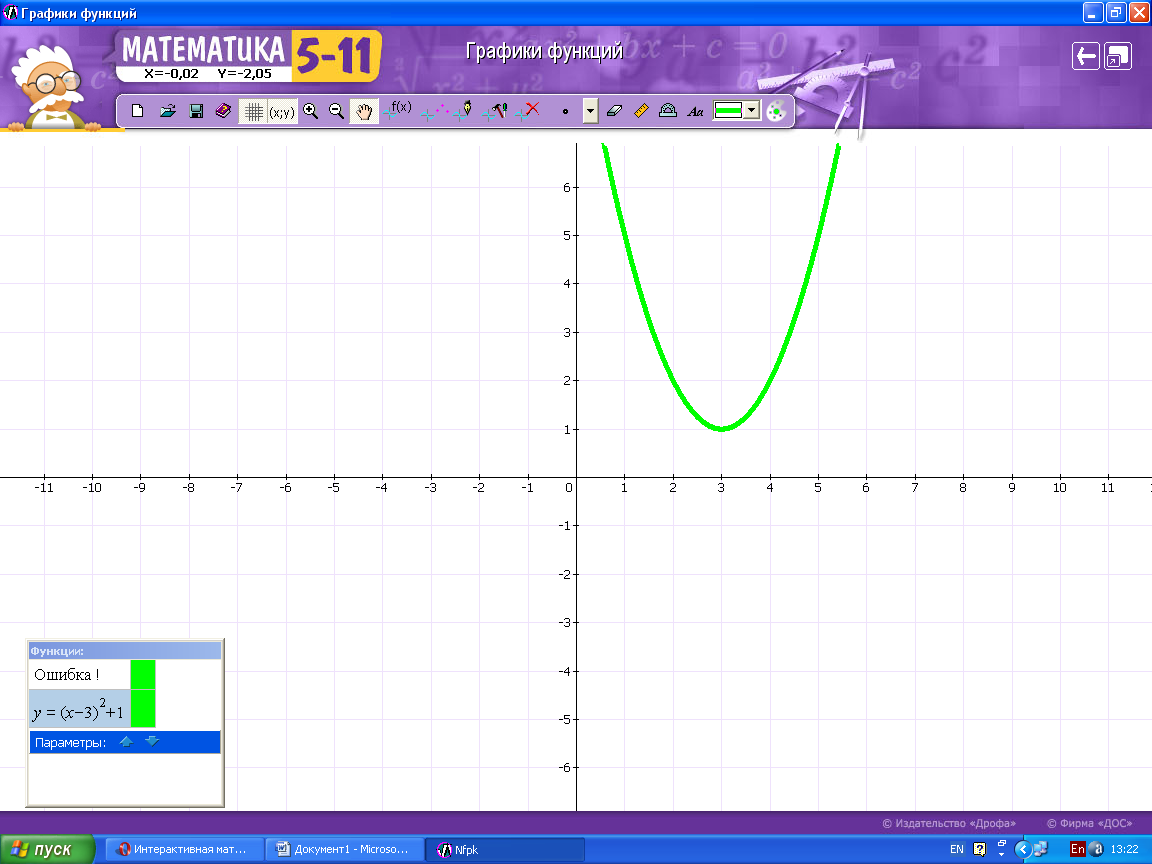
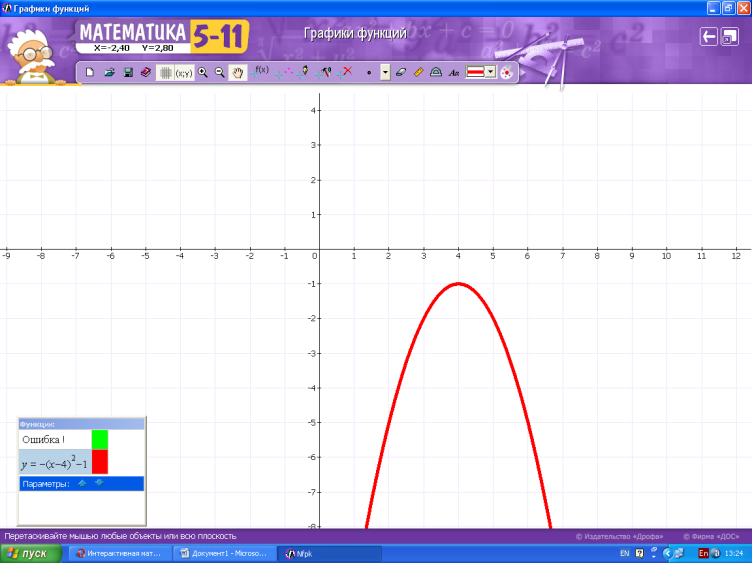
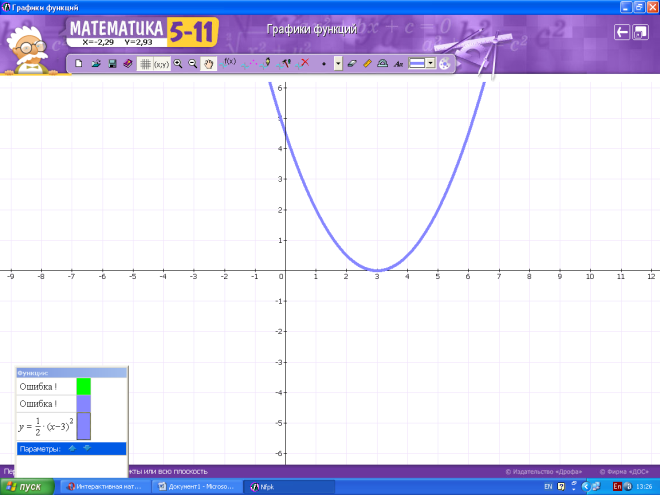
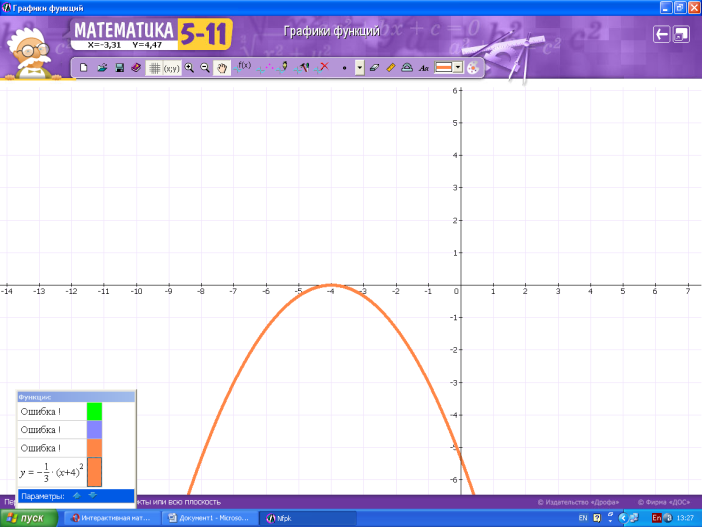
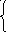 2 + 5х +6 ≥ у;
2 + 5х +6 ≥ у;