Тема урока: «Определение арифметической прогрессии, формула n-го члена».
Цели и задачи урока:
Дать определение арифметической прогрессии, вывести формулу n-го члена арифметической прогрессии , учить учащихся применять ее при решении упражнений.
Продолжить работу над развитием мыслительной деятельности учащихся: умением анализировать, сравнивать, делать выводы.
Продолжить работу над развитием речи, в том числе и математической, развивать умение слушать и слышать учителя, учиться взаимопониманию и уважительному отношению друг к другу.
Ход урока.
Организационный момент.
- Здравствуйте ребята. Садитесь. Дежурный назовите отсутствующих. Проверьте свою готовность к уроку – наличие на столе учебника, тетради, ручки, карандаша и конечно дневника. Далее сообщаю тему и ход урока урока
2. Проверка домашнего задания.
(Было задано №15.20, №15.31(а,б), №15.33)
Какие задания домашней работы вызвали затруднение? ( если такие есть, то просматриваем слайды 1,2,3)
3. Изучение нового учебного материала.
- Устный опрос : 1. Вспомните определение числовой последовательности (функцию вида у = f(x), где х є N, называют числовой последовательностью и обозначают у = f(x) или  (слайд 4)
(слайд 4)
2.Какие способы задания последовательности вы знаете? (аналитический, словесный, рекуррентный)(слайд 5)
3. Дайте определение возрастающей прогрессии (последовательность (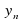 ) называют возрастающей, если каждый ее член ( кроме первого) больше предыдущего)(слайд 6)
) называют возрастающей, если каждый ее член ( кроме первого) больше предыдущего)(слайд 6)
4. Дайте определение убывающей прогрессии (последовательность (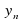 ) называют убывающей, если каждый ее член ( кроме первого) меньше предыдущего)(слайд7)
) называют убывающей, если каждый ее член ( кроме первого) меньше предыдущего)(слайд7)
Рассмотрим последовательности натуральных чисел : 1) 1; 5; 9; 13; 17; 21;…
2) -2; -4; -6; -8; -10; …
Назовите первый член последовательности, третий член, седьмой ? Как вы нашли седьмой член последовательности?( 1)- увидели, что каждое следующее число увеличивается на 4, 2)- увидели, что каждое следующее число уменьшается на 2). Эти последовательности являются примером арифметической прогрессии.(слайд №8)
Другими словами последовательность (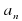 )- арифметическая прогрессия, если для любого натурального числа n выполняется условие
)- арифметическая прогрессия, если для любого натурального числа n выполняется условие 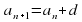 , где d –некоторое число, которое называют разностью арифметической прогрессии. Отсюда d=
, где d –некоторое число, которое называют разностью арифметической прогрессии. Отсюда d= 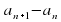 (слайд №9).
(слайд №9).
Откройте учебники на странице 146, рассмотрим примеры 1,2,3. Назовите  и d. Какой будет арифметическая прогрессия в первом примере? (возрастающая), а во втором ? (убывающая) слайд №10
и d. Какой будет арифметическая прогрессия в первом примере? (возрастающая), а во втором ? (убывающая) слайд №10
Арифметическая последовательность может быть бесконечной, обозначается так:
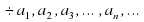 и конечной
и конечной 
Зная,  и d можно найти следующие члена последовательности, но если нужно найти
и d можно найти следующие члена последовательности, но если нужно найти 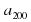 , то этот способ не удобен. Эти вычисления можно упростить, если вывести формулу n-го члена, то есть задать функцию аналитически.
, то этот способ не удобен. Эти вычисления можно упростить, если вывести формулу n-го члена, то есть задать функцию аналитически.
Рассмотрим арифметическую прогрессию : 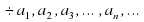 с разностью d .Найдем последовательно
с разностью d .Найдем последовательно 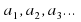
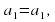

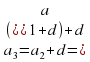 =
= 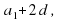

 =
=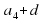 =
=  +
+ =
= 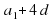 и т. д.
и т. д.
Нетрудно догадаться что 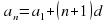 - это формула n-го члена арифметической прогрессии.(слайд 11)
- это формула n-го члена арифметической прогрессии.(слайд 11)
4. Закрепление учебного материала.
А сейчас открываем задачники и начинаем работать с заданиями.
Устно №16.1 Среди заданных последовательностей выберете арифметическую прогрессию:
Ответ: а, б, в.
№ 16.3(в,г)
В тетрадях №16.5(а,в), №16.13(а,в), №16.16(в),
Решите задачу: №1Бригада стеклодувов изготовила в январе 80 изделий, а в каждый следующий месяц изготовляя на 17 деталей больше , чем в предыдущий .Сколько деталей изготовила бригада в июне?
№2Отдыхающий, следуя совету врача, в первый день загорал 5 минут. А в каждый последующий день увеличивал время пребывания на солнце на 5 минут. На какой день время пребывания на солнце будет равно
40 минут?
(аn=а1+d(n+1), 40=5+5(n-1), 5n=40, n=8. Ответ: на восьмой день.)
Физкультминутка.
Это упражнение улучшит кровообращение вашего мозга.
Ленивые восьмерки. Поставьте большой палец правой руки. Пальцем в воздухе пишем восьмерки, следим за пальцем глазами. Затем другой рукой. Обеими руками.
Сгибание шеи. Скрестив пальцы на затылке, поднять голову, смотреть вверх, согнуть шею смотреть вниз. Повторить 5 раз.
Чтобы успешно завершить наш урок, давайте немного повторим.
Дайте определение арифметической прогрессии (слайд8)
(Арифметической прогрессией называется последовательность, каждый
член которой, начиная со второго, отличается от предыдущего на одно и
то же число)
Как проверить, является ли последовательность арифметической прогрессией? (слайд 11)
(Каждый член арифметической прогрессии больше предыдущего на одно
и тоже число.)
Проверьте: является ли последовательность арифметической прогрессией: (слайд 12)
-2; -4; -6; -8; -10;…
-13; -3; 13; 23;…
(Первая последовательность является арифметической, а вторая – нет).
- Назовите первый член этой прогрессии?
(а1=-2)
- Чему равна разность этой прогрессии?
(d=-2)
- Назовите шестой член этой прогрессии.
(а6=-12)
4. Укажите формулу n-го члена арифметической прогрессии (слайд 13)
А. аn=а1+(n+1), Б. аn=2а1+(n+1)d, В. аn=2а1+(n-1)d, Г. аn=а1+(n-1)d
(Вариант Г)
Мы сегодня хорошо поработали , молодцы ребята! У вас на столе лежат карточки трех цветов. Выберите ту которая соответствует вашему настроению на уроке.( слайд 14) Если кто-то что-то не понял выясняю причину и оставляю поработать после урока.
4.Задание на дом
А теперь домашнее задание: повторить п. 15, изучить п.16, №16.4, №16.12(а,б), №16.7, для сильных учеников № 16.14.
Урок окончен! Спасибо за внимание!
 (слайд 4)
(слайд 4)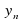 ) называют возрастающей, если каждый ее член ( кроме первого) больше предыдущего)(слайд 6)
) называют возрастающей, если каждый ее член ( кроме первого) больше предыдущего)(слайд 6)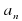 )- арифметическая прогрессия, если для любого натурального числа
)- арифметическая прогрессия, если для любого натурального числа 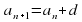 , где
, где 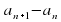 (слайд №9).
(слайд №9). и
и 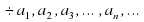 и конечной
и конечной 
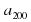 , то этот способ не удобен. Эти вычисления можно упростить, если вывести формулу
, то этот способ не удобен. Эти вычисления можно упростить, если вывести формулу 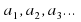
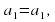

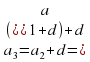 =
= 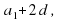

 =
=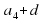 =
=  +
+ =
= 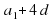 и т. д.
и т. д.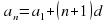 - это формула
- это формула 









 0, и убывающей, если d
0, и убывающей, если d


























