Урок по алгебре. Тема: "Тригонометрические функции числового аргумента"
Цели урока:
Образовательные:
Выработка умений и навыков применения тригонометрических формул для упрощения тригонометрических выражений.
Добиться понимания учащимися соотношений между функциями одного и того же аргументы
Сформировать умение применять изученные соотношения для тождественных преобразований выражений, нахождению значений тригонометрических функций по заданному значению одной из них.
Развивающие:
развивать внимание, ясность и точность мысли, умение рассуждать,
реализация принципа деятельностного подхода в обучении учащихся, развитие коммуникабельности и толерантности учащихся, умения слушать и слышать других и высказывать своё мнение.
развивать интуицию и логическое мышление, умение выделять существенные признаки математического понятия, сравнивать и обобщать, самостоятельно выполняя задания
развивать элементы алгоритмической культуры, умение планировать и контролировать свою деятельность, работать в заданном времени,
развивать умение оценивать свои знания и возможности, способность преодолевать трудности.
Воспитательные:
воспитывать ценностное отношение к предмету, интерес к его изучению и понимание значимости предмета, через иллюстрацию прикладного характера математики,
воспитывать аккуратность, добросовестное отношение к работе, уважительное отношение к товарищам, умение работать самостоятельно, в парах и коллективе,
формировать систему нравственного отношения к себе, одноклассникам, школе и обществу
Тип урока: урок отработки навыков и умений
Технология урока: групповое обучение.
Тип групп: группа, сидящая вместе. Ученики разного уровня обученности, информированности по данному предмету, совместимые учащиеся, что позволяет им взаимно дополнять и обогащать друг друга.
Ход урока
Ученики сидят по группам: 4 группы по 5-6 человек. Каждая группа – это экипаж яхты с названиями, соответствующими названиям тригонометрических функций, во главе с рулевым. Каждому экипажу выдаётся маршрутный лист и определяется цель: пройти заданный маршрут успешно, без ошибок. Урок сопровождается презентацией.
I. Организационный момент.
Цель: Подготовить к успешному выполнению заданий на уроке.
Учитель сообщает тему урока, цель урока, ход урока, план работы групп, роль капитанов.
Вступительное слово учителя:
– Ребята! Запишите число и тему урока: «Тригонометрические функции числового аргумента».
Сегодня на уроке мы будем учиться:
Вычислять значения тригонометрических функций;
Упрощать тригонометрические выражения.
Для этого нужно знать:
Определения тригонометрических функций
Тригонометрические соотношения (формулы).
Известно давно, что одна голова хорошо, а две лучше, поэтому вы сегодня работаете в группах. Сегодня урок у нас пройдёт в виде игры «Математическая регата». Каждая группа – это экипаж яхты, во главе с капитаном.
Цель игры:
Название экипажей соответствует марке яхты, на которой вы совершаете пробег.
Представляются экипажи и их капитаны:
Экипаж – «Синус»
Экипаж – «Косинус»
Экипаж – «Тангенс»
Экипаж – «Котангенс»
Девиз гонки: «Тише едешь – дальше будешь!»
Вам предстоит совершить гонку по «математическому океану» с множеством препятствий.
Маршрутные листы каждому экипажу выданы. Преодолеть препятствия смогут экипажи, которые знают определения и тригонометрические формулы.
Во время пробега каждый капитан руководит экипажем, помогая, и оценивая вклад каждого члена экипажа в преодоление маршрута в виде «плюсов» и «минусов» в оценочном листе. За каждый правильный ответ группа получает «+», неправильный «-».
Вам предстоит преодолеть следующие этапы пути:
I этап. Правила движения на воде
II этап. Техосмотр.
III этап. Соревнования – гонка между яхтами
IV этап. Внезапная остановка – авария.
V этап. Отдых в Голубой бухте.
VI этап. Финиш.
VII этап. Итоги.
И так в путь!
I этап. Правила движения на воде.
1) В каждом экипаже капитаны раздают каждому члену экипажа билеты с теоретическими вопросами:
Расскажите определение синуса числа t и его знаки по четвертям.
Расскажите определение косинуса числа t и его знаки по четвертям.
Назовите наименьшее и наибольшее значения sin t и cos t.
Расскажите определение тангенса числа t и его знаки по четвертям.
Расскажите определение котангенса числа t и его знаки по четвертям.
2) Математическое лото. Соберите «рассыпавшиеся» формулы. В конверте карточки с написанными формулами. Экипажи должны привести в соответствие формулы. Ответ каждая команда записывает на демонстрационном листе в виде строки соответствующих букв (парами).
| А | 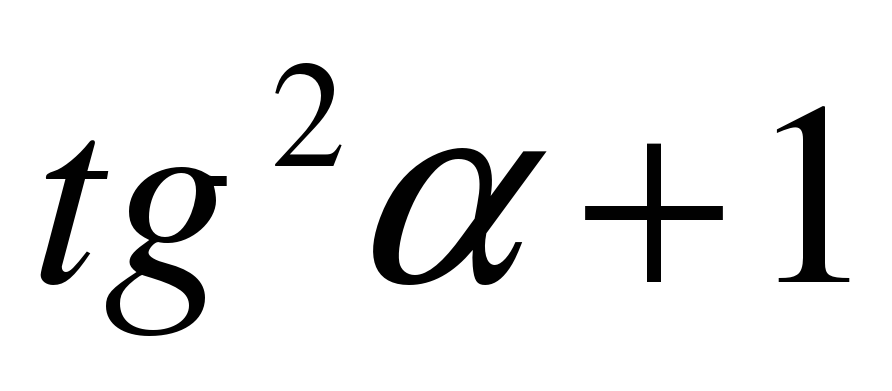 | Е | 1 |
| В | 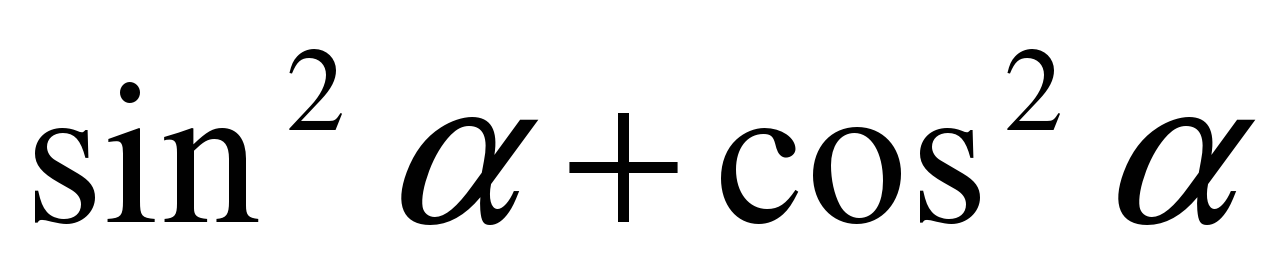 | Ж | 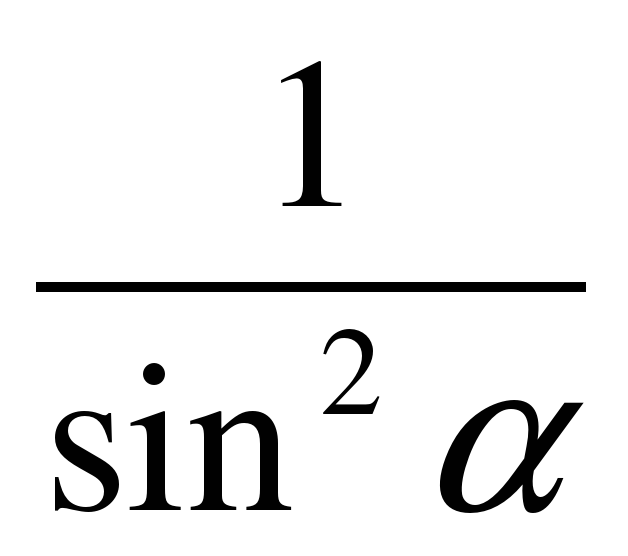 |
| Д | 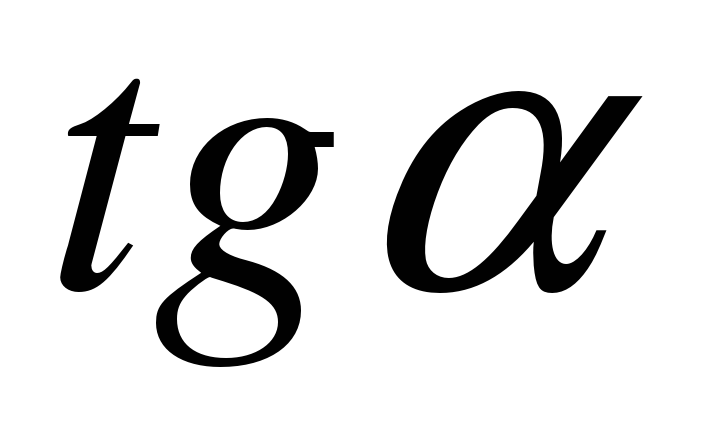 | И | 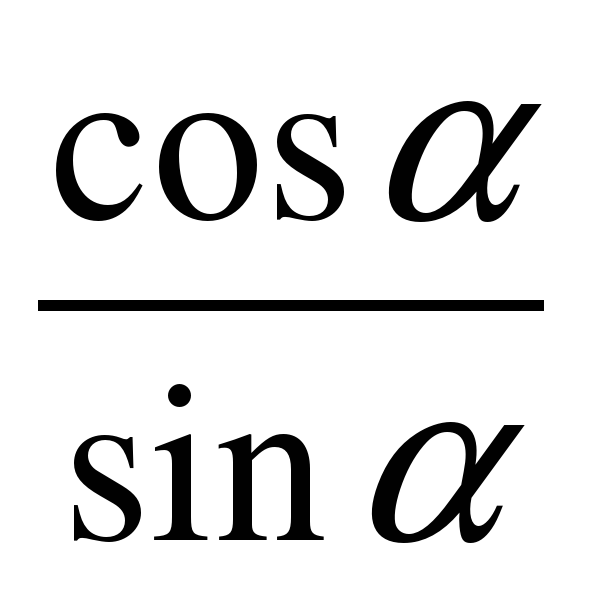 |
| Л | 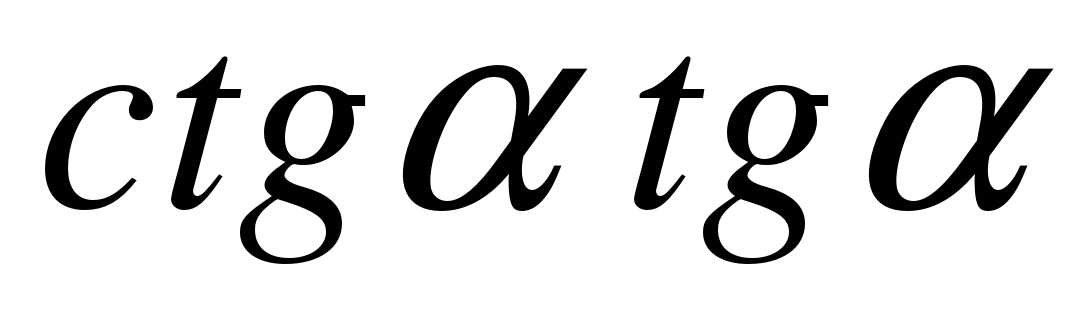 | К | 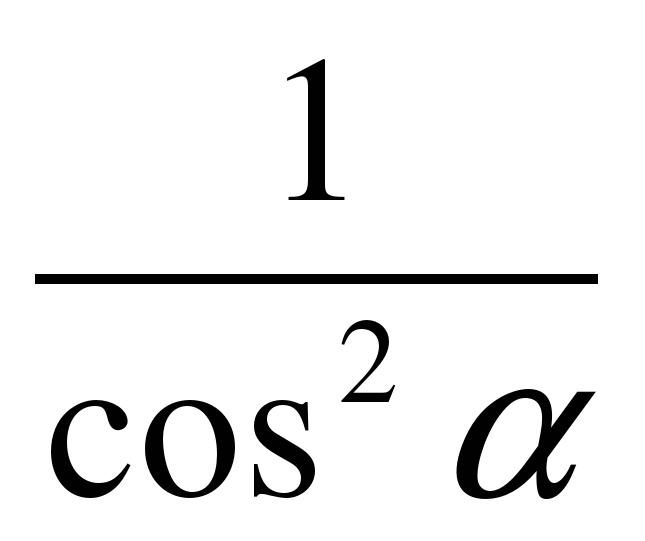 |
| З | 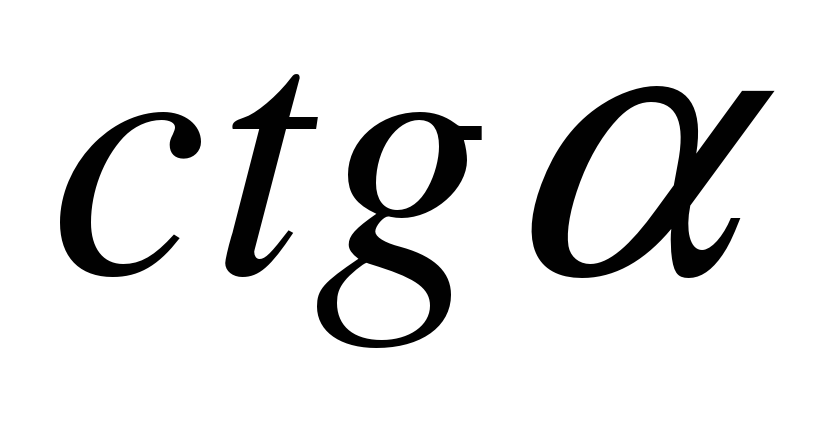 | Г | 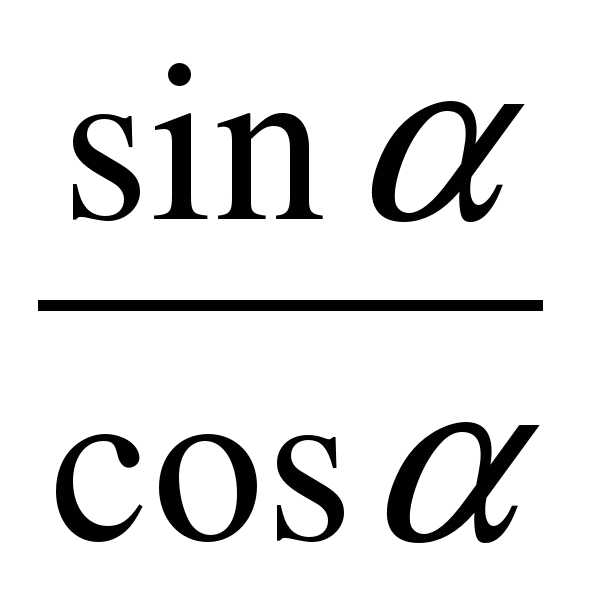 |
| Й | 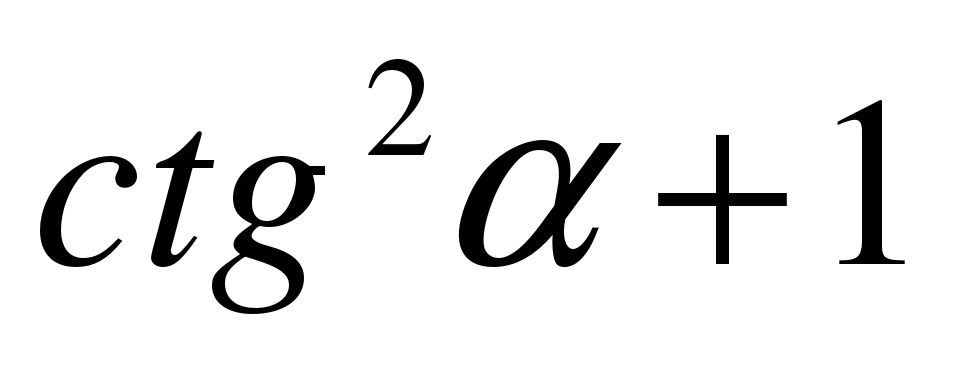 | Б | 1 |
Ответ: АК; ВЕ; ЛБ; ДГ; ЗИ; ЙЖ
II этап. Техосмотр.
Цель: Повторить основное тригонометрическое тождество.
Устная работа: тест.
Каждый экипаж получает листок, на котором написано задание: упростить выражение.
Рядом записаны варианты ответов. Экипажи определяют правильные ответы за 1 мин. и поднимают соответствующий набор букв.
| № | Выражение | Варианты ответов |
| А | В | С |
| 1. | 1 – cos2t | cos2t | - sin2t | sin2t |
| 2. | sin2t – 1 | cos2t | - cos2t | 2 cos2t |
| 3. | (cos t – 1)(1+ cos t) | -sin2t | (1+ cos t)2 | (cos t – 1)2 |
Ответ: С В А.
III этап. Гонка с препятствиями
3 минуты экипажам на совещание по решению задания, а далее представители экипажей пишут решение на доске. Когда представители экипажей закончат записывать решение первого задания, все ученики (вместе с учителем) проверяют правильность и рациональность решений и записывают в тетрадь. Капитаны оценивают вклад каждого члена экипажа знаками « + » и « – » в оценочных листах.
Задания из учебника: № 3, стр.277
Экипаж – «Синус»: № 3(1,2,3);
Экипаж – «Косинус»: № 3 (4,5);
Экипаж – «Тангенс»: № 3 (6);
Экипаж – «Котангенс»: № 3 (7).
IV этап. Внезапная остановка – авария.
– У вашей яхты проблемы с двигателем. Необходимо выполнить мелкий ремонт, а для этого каждый экипаж должен ответить на поставленный вопрос.
V этап. Отдых в Голубой бухте
Вы устали и должны отдохнуть. Пока экипаж отдыхает, капитаны подводят предварительные итоги: считают «плюсы» и «минусы» у членов экипажа и в целом у экипажа.
Для учеников:
3 и более «+» – оценка «10»;
2 «+» – оценка «8»;
1 «+» – оценка «5».
Для экипажей: «+» и «-» взаимно уничтожаются. Считаются только оставшиеся знаки.
Отгадайте шараду.
Из чисел вы мой первый слог возьмите,
Второй – из слова «гордецы».
А третьим лошадей вы погоните,
Четвёртым будет блеянье овцы.
Мой пятый слог такой же, как и первый,
Последней буквой в алфавите является шестой,
А если отгадаешь ты всё верно,
То в математике раздел получишь ты такой.
(Три-го-но-ме-три-я)
Слово «тригонометрия» (от греческих слов «тригонон» – треугольник и «метрео» – измеряю) означает «измерение треугольников». Возникновение тригонометрии связано с развитием географии и астрономии – науки о движении небесных тел, о строении и развитии Вселенной.
VI этап. Финиш. Самостоятельная работа
Цель: обобщение знаний, полученных на уроке, анализ овладения способами деятельности.
Самостоятельную работу экипажи выполняют по вариантам (учитель раздает задание на листочках)
(выполнение самостоятельной работы поможет вам в выполнении №2 стр 245 из домашнего задания)
Вариант «Синус»:
Укажите, какой знак имеет выражение:
а) cosα, если α – угол II координатной четверти;
б) sin185º;
в) ctg204ºsin164º;
г) sin(-230º) ∙ cos(-300º) ∙ tg155º
2. Найдите значение выражения:
а) cos(360º + 45º);
б) ctg(540º - 30º);
в) sin405º;
г) tg(-900)º
Вариант «Косинус»:
Укажите, какой знак имеет выражение:
а) sinα, если α – угол III координатной четверти;
б) cos1705º;
в) cos356º∙tg100º;
г) sin275º ∙ tg(-300º) ∙ cos(-50º)
2. Найдите значение выражения:
а) sin(360º + 30º);
б) cos(720º - 30º);
в) tg225º;
г) ctg(-570)º
Вариант «Тангенс»:
Укажите, какой знак имеет выражение:
а) tgα, если α – угол IV координатной четверти;
б) sin335º;
в) cos230º∙ctg179º;
г) cos (-350º) ∙ sin(-278º) ∙ tg48º
2. Найдите значение выражения:
а) tg(180º + 60º);
б) sin(720º - 30º);
в) ctg150º;
г) cos(-765º)
Вариант «Котангенс»:
Укажите, какой знак имеет выражение:
а) сtgα, если α – угол I координатной четверти;
б) sin230º;
в) cos260º∙sin190º;
г) cos (356º) ∙ sin(-108º) ∙ tg(-100º)
2. Найдите значение выражения:
а) ctg(180º + 30º);
б) cos(720º + 45º);
в) ctg(-780º);
г) cos540º
Учитель собирает листочки, проверяет, оценивает и объявляет оценку за самостоятельную работу на следующем уроке. Критерии оценивания:
а) за правильные ответы а и б по 0,5 балла ;
б) за правильные ответы в по 2 балла;
в) за правильные ответы г по 3 балла;
VII этап. Итоги.
Итоги игры.
Капитаны сдают оценочные листы. Определяется экипаж, ставший чемпионом «Математического ралли» и характеризуется работа остальных групп. Далее называются фамилии тех, кто получил оценки «10» и «9».
Итоги урока.
– Ребята! Чему вы сегодня научились на уроке? (упрощать тригонометрические выражения; находить значения тригонометрических функций). А что для этого нужно знать?
определения и свойства sin t, cos t, tg t, ctg t;
соотношения, связывающие значения различных тригонометрических функций;
знаки тригонометрических функций по четвертям числовой окружности.
значения тригонометрических функций первой четверти числовой окружности.
– Я думаю, что вы поняли, что формулы нужно хорошо знать, чтобы их правильно применять. Вы также поняли, что тригонометрия очень важная часть математики, так как она применяется в других науках: астрономии, географии, физике и др.
Рефлексия
Чтобы показать учащимся, как они работали в группе, каков уровень их коммуникации, анализируется не только результат, но и процесс работы, который оценивается по следующему алгоритму:
(раздается каждому ученику в виде анкеты)
Как общение в ходе работы влияло на выполнение задания?
делало её более эффективной
тормозило выполнение задания
не позволило точно выполнить задачу, испортило отношения в группе
На каком уровне в большей степени осуществлялось общение в группе?
Какого уровня коммуникативные трудности испытывали участники группы при выполнении задания?
Какой стиль общения преобладал в работе?
Сохранилось ли единство группы в ходе выполнения задания?
Кто или что сыграло решающую роль в том, что произошло в группе?
лидер, выдвинувшийся в ходе работы
нежелание наладить контакт большинства участников группы
непонимание задачи, поставленной для совместной работы
сама задача оказалась неинтересной, трудной
Домашнее задание:
Цель: закрепление знаний, умений, навыков и самоконтроль.
Е.П. Нелин «Алгебра и начала анализа». Академический уровень, 10 класс: №№ 2,4, стр. 245




















