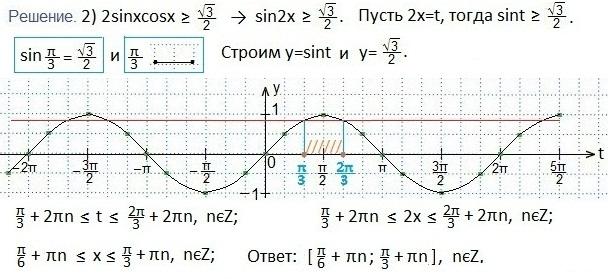
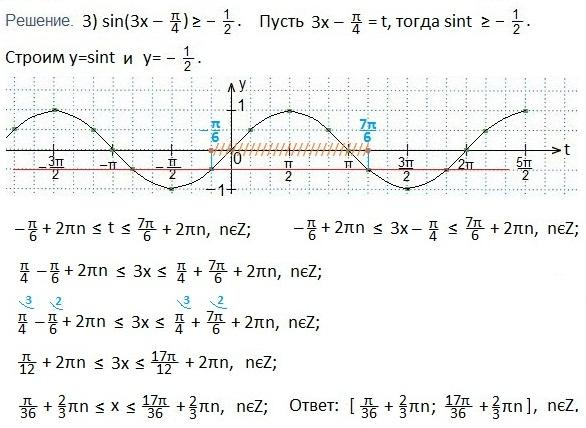
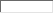
На прошлом занятии «10.2.1. Решение тригонометрических неравенств. Часть 1» мы решили три неравенства вида sint<a. На этом уроке мы рассмотрим три неравенства вида sint>a, где -1≤а≤1.
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается выше прямой у=а. Находим абсциссы этих точек.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Тригонометрическиt неравенствa Часть 2
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«тригонометрическиt неравенствa Часть 2 »
Полезное для учителя
Распродажа видеоуроков!
1310 руб.
1870 руб.
1750 руб.
2500 руб.
1490 руб.
2130 руб.
1750 руб.
2500 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
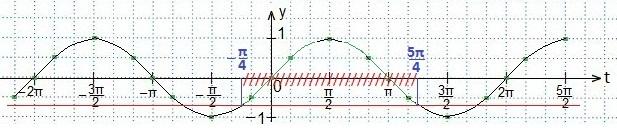
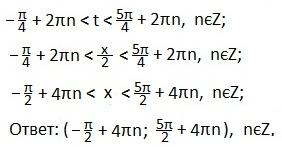 Учитывая периодичность функции синуса, запишем двойное неравенство для значений аргумента t, удовлетворяющий последнему неравенству. Вернемся к первоначальной переменной. Преобразуем полученное двойное неравенство и выразим переменную х.Ответ запишем в виде промежутка.
Учитывая периодичность функции синуса, запишем двойное неравенство для значений аргумента t, удовлетворяющий последнему неравенству. Вернемся к первоначальной переменной. Преобразуем полученное двойное неравенство и выразим переменную х.Ответ запишем в виде промежутка.