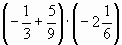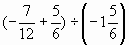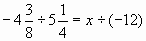Тема урока: Умножение положительных и отрицательных чисел.
Цель урока: умение выполнять учащимися умножение рациональных чисел
Задачи:
Создать условия для развития умений сравнивать, выявлять закономерности, обобщать, учить думать, высказывать свое мнение;
Воспитывать трудолюбие, аккуратность, умение работать коллективно.
Ход урока:
1. Организационный момент.
Приветствие учеников.
Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:
- Что есть больше всего на свете? – Пространство.
- Что быстрее всего? – Ум.
- Что мудрее всего? – Время.
- Что приятнее всего? – Достичь желаемого.
Хочется, чтобы каждый из нас на сегодняшнем уроке достиг желаемого результата.
Учащиеся становятся в круг и желают друг другу хорошего настроения.
2. Актуализация опорных знаний. Игра «Светофор»
Верно ли утверждение:
1) сумма двух чисел с разными знаками всегда положительна;
2) сумма двух чисел с разными знаками не всегда положительна;
3) сумма двух чисел с разными знаками всегда отрицательна;
4) сумма двух чисел с разными знаками не всегда отрицательна;
5) сумма двух чисел с разными знаками всегда равна нулю;
6) сумма двух чисел с разными знаками может быть равна нулю;
7) знак суммы двух чисел с разными знаками всегда такой же, как у слагаемого с большим модулем;
8) если модули слагаемых с разными знаками равны, то сумма слагаемых равна нулю;
9) сумма отрицательных чисел всегда отрицательное число.
Устный счет: игра с мячом: учитель бросает мяч и говорит задание, ученик мяч возвращает и говорит ответ
– 22 + 35 =
– 3,7 + 2,8 =
1,5 + (- 6,3) =
8,2 + (-8,2)=
22+(– 27)=
– 13+(– 8)=
19+ (- 2)=
27 + (- 3) =
-35 + 9=
-1,6 +(-4,7)=
2,5+(-3,6)=
Мотивация урока.
“Жил на свете богач, очень богатый богач, самый богатый на земле, но все ему казалось, что он еще недостаточно богат.
И вот однажды пришел к этому самому богатому богачу самый бедный бедняк на свете и сказал:
– О, господин! Сияние твоих сокровищ слепит глаза. И все-таки у меня есть способ умножить твое богатство. А заодно и свое.
Богач прямо затрясся от жадности:
– Чего ты стоишь? Умножай скорее!
– А ты не будешь на меня в обиде? – опасливо спросил бедняк.
– Да ты что! Ведь ты хочешь умножить мое богатство!
– Конечно, умножить, – подтвердил бедняк.
– Так умножай, и дело с концом! – закричал богач, теряя терпение.
– Быть по-твоему, – ответил тот. – Раз, два, три! Готово!
Богач бросился к своим сундукам да как закричит:
– Что ты наделал, негодный?! Ты меня разорил! Где мое золото? Где алмазы? Где жемчуга?
– Были у тебя, теперь они у меня, – сказал бедняк.– Ведь ты же сам просил меня умножить! Я и умножил.″ Как так получилось, как вы думаете?
4. Изучение нового материала.
Создание проблемной ситуации.
Как вы думаете, почему так получилось?
Какое действие с числами нужно знать, что бы ответить на этот вопрос? (умножение)
А вы знаете, как выполняется умножение чисел? (натуральных и дробных положительных, да)
Тогда какая задача нашего сегодняшнего урока, что бы вы хотели узнать? (как умножить положительные и отрицательные числа)
А какие числа еще можно перемножать? (отрицательные)
Итак, тема нашего урока: «Умножение положительных и отрицательных чисел».
Вспомните, пожалуйста, какие методы мы использовали при выведении правил сложения и вычитания натуральных чисел и предложите свои версии, как нам получить правила умножения чисел.
Версии фиксируются на доске и в тетрадях.
Использовать термометр и рассмотреть умножение на примере изменения температуры.
Умножение заменить сложением.
Например, 4,5+4,5+4,5+4,5+4,5 можно заменить 4,5*5, а как быть, если -4,5+(-4,5)+(-4,5)+(-4,5)+(-4,5)?
Дети выдвигают предположения, но приходят к выводу , что -4,5*5 будет рациональней, чем складывать, и ответ получается отрицательным.
Просмотр видеоурока. Затем обсуждение просмотренного и коллективно под руководством учителя делаются выводы.
Выводы: 1) Произведение двух чисел одного знака положительно, а произведение двух чисел с разными знаками отрицательно;
2) Чтобы найти модуль произведения, нужно перемножить модули сомножителей.
Правила знаков при умножении
( + ) · ( + ) = ( + )
( - ) · ( - ) = ( + )
( + ) · ( - ) = ( - )
( - ) · ( + ) = ( -)
Давайте вернемся к сказке, которую вы услышали в начале урока. Можете ли вы сейчас ответить на вопрос, почему богач лишился своего богатства, на какое число бедняк умножил богатство богача?
Устная работа. (Флипчарт или презентация))
Сравните с нулём:
( -1-2-3-4-5-6-7 )·(-157 ) и 0
( 1+2+3+4+5+……99) · ( 300-1) и 0
(-1) · (-2) · (-3) · …. · (-10) и 0
(-2) · (-4) · (-6) · …. · (-102) и 0
2.
3. Вставить пропущенные числа
0,5 · * = - 20
-1,25 · * = 2,5
- 0,8 · * = - 4
Вычислить удобным способом
(-1) · 2 · (-3) · 4 (-5) · ½ · (- 1/3) · ¼ · ( - 1/5) =
(-2) · (-4) · 0,5 · (-0,25) · (-6) =
4.Не производя вычислений, укажите верные утверждения:
а) значение выражения (-2)(-3)5,5 – отрицательное число;
б) значение выражения (-2,2)(-3,5)(-6) – отрицательное число;
в) значение выражения (-5,3)7(-2,3) – положительное число;
г) значение выражения (-9)(-2)6 – отрицательное число
Самостоятельная работа.– А сейчас задание: определить знак произведения и вычислить.
а) (-7) · (-5) · 2 = 70
(-4) · (-10) · 8 = 320
б) (-2) · (-3) · (-4) = – 24
(-1,2) · (-2) · (-12)= – 28,8
в) (-1) · (-2) · (-5) · (-15) · 2 = 300
– Какой вывод можно сделать относительно знака произведения, где чётное (нечётное) число отрицательных множителей?
Вывод: 1. Если число отрицательных множителей нечетное, то произведение - число отрицательное.
2. Если число отрицательных множителей чётное, то произведение - число положительное.
6. Физминутка.
Мы с вами посмотрели, где можно встретиться с положительными и отрицательными числами. Наряду с положительными и отрицательными числами есть понятие положительных и отрицательных качеств человека. Если качество положительное, то показываете “+”, если отрицательное, то “–”.
Доброта, лень, предательство, трудолюбие, жестокость, целеустремленность, усидчивость.
Мне очень хотелось бы, чтобы положительных качеств было как можно больше.
8. Итоги урока. Рефлексия
– А теперь давайте попытаемся понять, что же каждому из нас дал сегодняшний урок. Интересно ли вам сегодня было? Чему научились? Что вызвало затруднение?
И завершить наш урок я хочу пожеланием каждому из вас:
"К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай".
Д/з Самостоятельная работа в форме теста:
I – вариант
1. Вычислите: - 8,7 – (3,6 – 8,7)
1) -3,6; 2) -13,8; 3) 3,6; 4) 13,8.
2. Выполните действия: 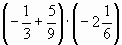
1) 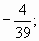 2)
2) 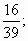 3)
3) 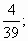 4)
4) 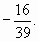
3. Выполните действия: -6 · (-5 + 21) : 32 + 8
1) 3; 2) -5; 3) 11; 4) 5.
4. Решите уравнение: х : (-16) = 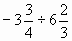
1) 10; 2) 9; 3) - 9; 4) – 10.
II – вариант
1. Вычислите: - 7,8 – (9,1 – 7,8)
1) 9,1; 2) -6,5; 3) -9,1; 4) 6,5.
2. Выполните действия: 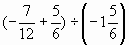
1) 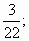 2) -
2) -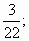 3)
3) 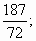 4)
4) 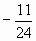 .
.
3. Выполните действия: -8. (-7 + 23) : 64 + 3
1) 5; 2) 10,5; 3) -4,5; 4) 1.
4. Решите уравнение: 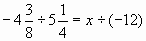
1) 2,5; 2) 10; 3) 14,4; 4) 15.