8
Тема урока: Пирамида
Цель урока: обеспечить усвоение студентами знаний о пирамиде и формирование умений применять эти знания на практике при построении чертежей и решении простых задач
Задачи:
актуализировать знания студентов о видах изученных многогранников, их элементах;
совершенствовать умения определять вид многогранников по чертежам и моделям, а также составлять и решать простейшие геометрические задачи по чертежам;
формировать представления студентов о пирамиде (ввести определение, обозначение пирамиды, рассмотреть её основные элементы, виды, свойства правильной пирамиды, вывести формулы площадей полной и боковой поверхности);
формировать умения студентов определять вид пирамиды; строить чертежи пирамиды по заданным условиям и решать простые задачи по данной теме;
развивать пространственное воображение, грамотную математическую речь, умения слушать, анализировать, строить логические цепочки, делать выводы;
воспитывать эмоционально-положительное отношение к изучению геометрии; умение быстро, грамотно и аккуратно оформлять записи в своих конспектах, работать в коллективе.
Тип урока: изучение нового материала
Временные рамки: 2 урока по 45 мин.
Формы работы учащихся: фронтальная, групповая, индивидуальная
Необходимое оборудование и технические средства:
персональный компьютер;
мультимедийный проектор;
экран;
учебная презентация;
таблица «Знаю, узнал, научился» - для каждого студента;
модели многогранников,
пластилин, палочки, картон, ножницы (по количеству групп),
карточки с заданиями для групповой работы,
карточки с простыми задачами,
линейка, цветной мел,
карточки с домашним заданием.
Ход урока
Организационный момент (отсутствующие, готовность к уроку).
Работа на уроке будет осуществляться фронтально и группах.
2. Сообщение темы и целей урока
Сегодня на уроке мы рассмотрим еще один вид многогранников. Послушайте стихотворение:
Стоит на земле пирамида,
и Боги о ней говорят.
На ней не рванье, не хламида,
а вечного камня наряд.
Она здесь стоять не устала,
хоть минуло много веков.
Она головою достала
до самых, седых облаков.
Что людям она сохранила?
Великих камней забытьё?
Зрачки желтоглазого Нила
лениво глядят на нее.
Эпиграфом к сегодняшнему уроку станет высказывание арабского писателя 13 века : «Все на свете боится времени, а время боится пирамид”.
Вы наверное поняли, что речь пойдет о пирамидах. Их наделяют многими магическими свойствами, о них существует много гипотез и легенд.
Итак, тема урока «Пирамида» (слайд 2) . Мы рассмотрим следующие вопросы:…
Целями нашего урока будут: …. (слайд 3)
3. Актуализация знаний и повторение материала.
Но прежде чем говорить непосредственно о пирамидах, предлагаю освежить в памяти уже знакомый вам материал.
Задание 1
Перед вами таблица «Знаю, узнал, научился». Заполните первый столбец таблицы. Для этого поставьте в первом столбце любой значок напротив известных вам фактов.
Задание 2
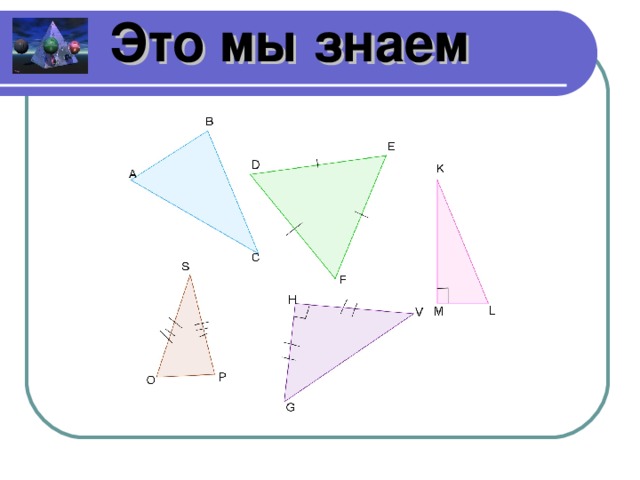
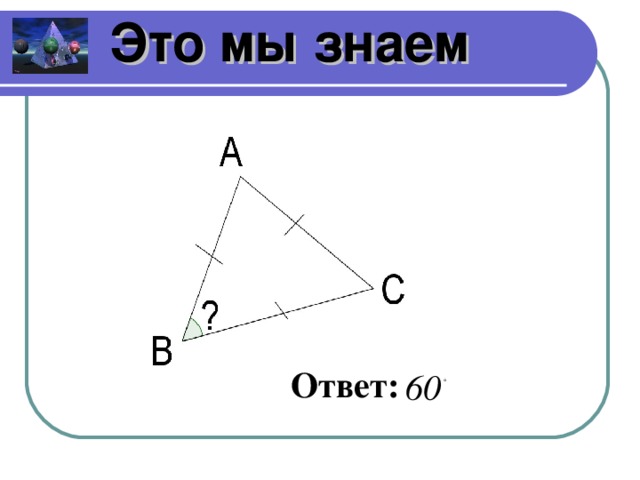
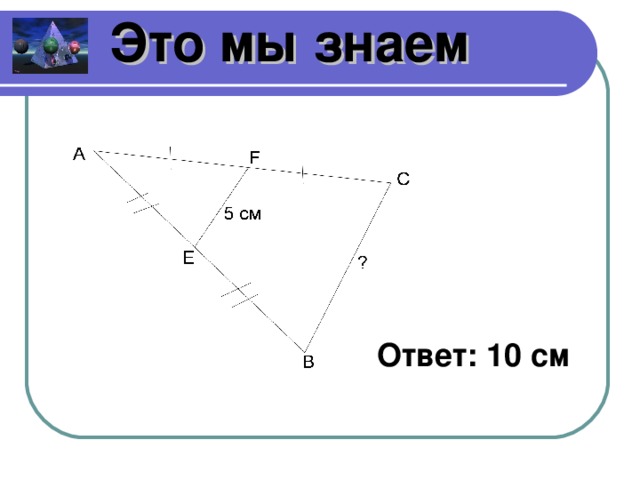
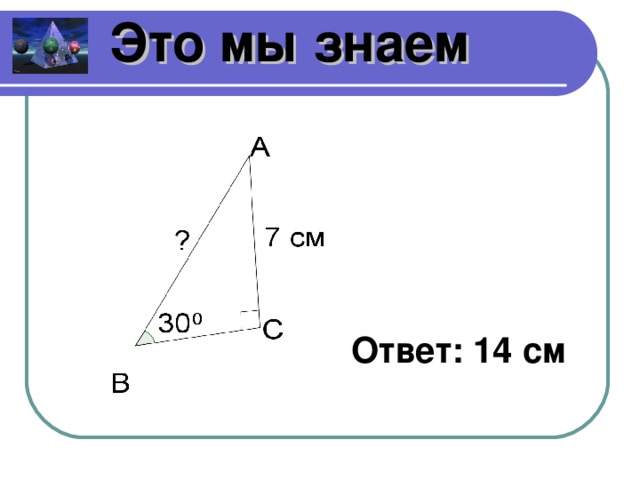
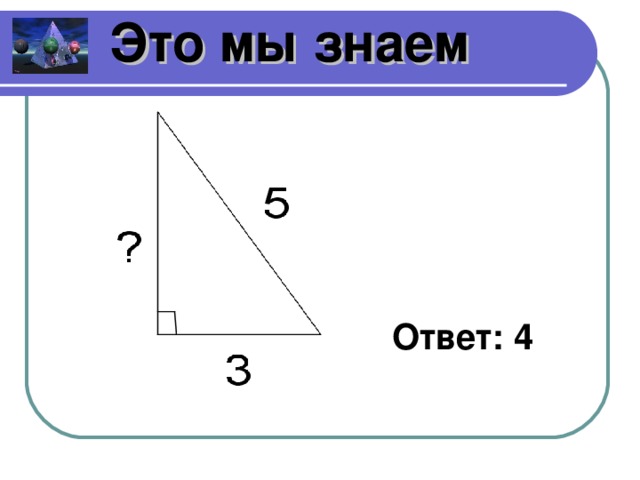
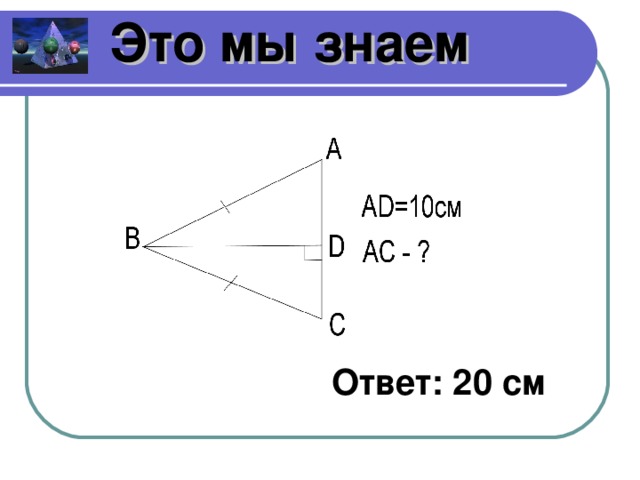
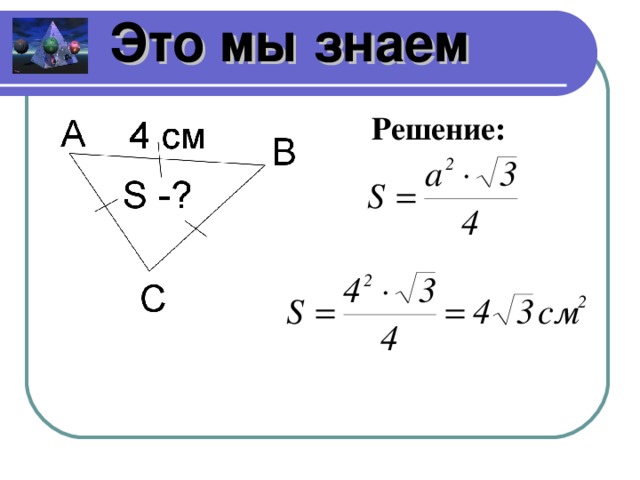
Вспомним, что мы знаем о треугольниках. Чертежи (слайды 4- 10)
Какие треугольники изображены и почему? (прямоугольные, равнобедренные, равносторонние, произвольные)
Составьте и решите по чертежу задачу для других групп. Группа, ответившая правильно составляет следующую задачу. Если никто не отвечает, отвечаете сами. Тогда следующую задачу составляет следующая группа.
Начинаем с той, которая наиболее активно отвечала на первый чертеж.
Согласны ли вы с ответом? Есть ли у вас дополнения? Есть ли дополнение у других групп?
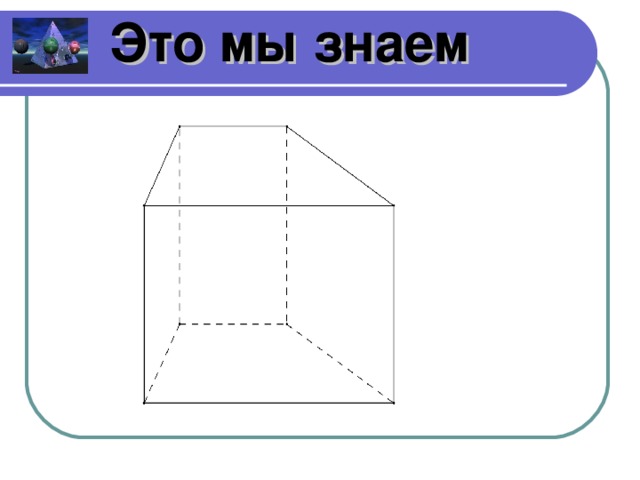
Задание 3. Назвать многогранник, объяснить почему (слайды 11-14)
Какие многогранники вы помните? Определите их название и вид по чертежу.
Показываются чертежи (предпоследним – лежащая 3-угольная призма, последним – пирамида).
Как называется последний многогранник?
(если скажут «призма») – Давайте сравним. Вспомните, из чего состоит призма? Найдите эти элементы на чертеже. Значит, данный многогранник призмой не является.
(если скажут «пирамида») – А может это призма? Посмотрите как данный многогранник похож на предыдущий. А в чем разница?
Итак, мы выяснили, что данный многогранник называется…. (пирамида).
Это тема нашего урока. Запишите ее в тетради. (слайд 15)
Изучение нового материала
Какие ассоциации вызывает у вас слово «пирамида»? Что вы знаете о пирамидах из жизни?
Давайте совершим небольшой историко – географический экскурс. Выступление учащихся с сообщениями:
Пирамиды – это единственное из семи чудес света чудо, дожившее до нашего времени, до эпохи телевидения и компьютерных технологий. Египетские пирамиды незыблемо высятся на фоне желто-коричневых песков Ливийской пустыни. К изучению пирамид приступили сравнительно недавно. Два века назад французский ученый Жомар, сопровождавший армию Наполеона в Египет, составил первое научное описание и провел первые точные измерения пирамид. Величайшая из пирамид – пирамида Хеопса в Египте. Она была построена в двадцать восьмом веке до н.э. Её создал племянник фараона по имени Хемиун. Высота этой пирамиды 147 м в древности и 138 м сейчас. Это соответствует современному зданию высотой около 50 этажей. Длина основания пирамиды 250 м. Основание этой пирамиды в два раза больше ширины Красной площади в Москве. Пирамида сложена из блоков золотистого известняка весом от 2,5 до 30 т. Глыбы со всех сторон гладко отшлифованы. Строителям пришлось обработать около 14 000 000 поверхностей, так как каждый монолит имел 6 граней. Все поверхности отшлифованы с такой математической точностью, что, соединив их, между ними нельзя просунуть тонкое лезвие ножа. Блоки ничем не скреплены и держатся на месте силой собственной тяжести. (слайд 16)
Пирамиды строили не только в Египте. Они вырастали и по другую сторону океана, в древних государствах Центральной Америки. К северу от Мехико ученые открыли обширный город Теотиукан, ошеломляющий пирамидами гигантских размеров. Самая большая – пирамида Солнца, периметр ее основания равен 1000 метров, а напротив нее возвышается пирамида Луны (на экране слайды с изображениями пирамид). Это мексиканские пирамиды.Подобные сооружения, созданные человеком и природой встречаются встречаются и в Китае, в Риме и даже на Украине. Пирамидальная форма широко используется в архитектуре, например во Франции, в Германии. (слайды 17 -18)
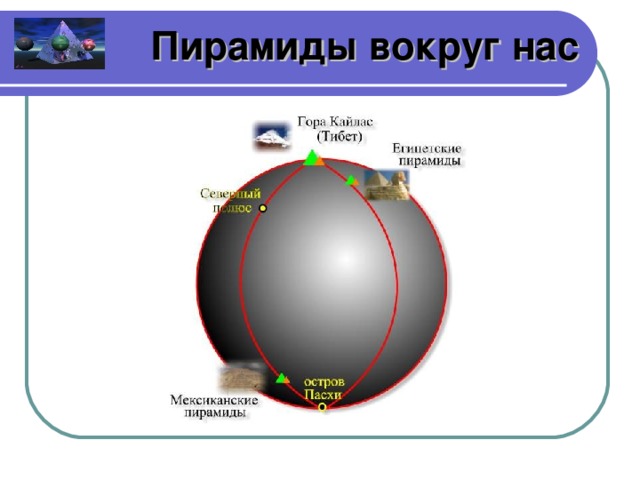
На Земле существует целая сеть пирамид. На фоне Гималайского хребта четко выделяется пирамидальное образование - гора Кайлас (слайд); Так вот, расположение г.Кайлас, египетских и мексиканских пирамид очень интересное, а именно (слайд) – если соединить г. Кайлас с мексиканскими пирамидами, то соединяющая их линия выходит на остров Пасхи. Если соединить г. Кайлас с египетскими пирамидами, то линия их соединения опять выходит на остров Пасхи. Если соединить мексиканские пирамиды и египетские, то мы получится два равных треугольника. Если найти их площади, то их сумма равна одной четвертой площади земного шара. (слайд 19)
Почему же именно эти сооружения получили названия пирамида? Что же означает это слово? Вот какие версии существуют. (сообщения учащихся)
Термин «пирамида» заимствован из греческого «пирамис» или «пирамидос». Греки в свою очередь позаимствовали это слово из египетского языка. В папирусе Ахмеса встречается слово «пирамис», означающее ребро правильной пирамиды. По другой версии, термин берет свое начало от формы хлебцев в Древней Греции («пирос» - рожь). По третьей версии слово «пирамида» в переводе с греческого 2 х слов: “pyra”- огонь, свет (или видимый) и “midos” – середина (внутри), звучит, как «светящиеся изнутри» . Дело в том, что до 1301-го года, когда после сильного землетрясения арабы стали использовать расшатавшуюся облицовку на строительство и восстановление дворцов и мечетей разрушенного Каира. Пирамида Хеопса была облицована плитами полированного известняка. Эти плиты были настолько блестящие, что могли быть замечены за сотни километров.
В Большом энциклопедическом словаре написано, что пирамида - монументальное сооружение, имеющее геометрическую форму пирамиды (иногда ступенчатую или башнеобразную). Сейчас слово «пирамида» определяет не только трехмерный треугольник. Его используют для обозначения любой твердой структуры, которая имеет широкую основу и поднимается, словно башня, сужаясь вверх.
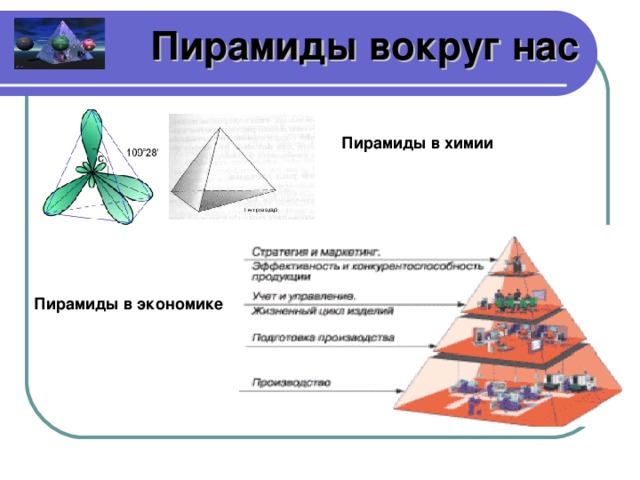
(слайд 20) Мы используем слово «пирамида», говоря о финансовых сделках, при которых доход от одной сделки применяется для вложения в другую и т. д.. существуют экологические пирамиды: численности, биомасс, энергии. Понятие пирамиды тесно связано с жизнью общества. Структуры государства (предприятия, школы, институты) напоминают собой пирамиды. Во всех этих понятиях используется структура, сужающаяся по мере роста.
Вывод: Итак – пирамида – это структура с широкой основой, сужающейся кверху.
Рассмотрим пирамиду с математической точки зрения. (слайды 21 - 22)
Что общего во всех этих определениях?
В наши дни определение пирамиды звучит так: (слайд 23) Запишите определение в тетрадь.
Давайте разберем определение на данных моделях
Из каких элементов состоит данная пирамида? (многоугольник, точка и отрезки)
Чем будет являться многоугольник? (основанием пирамиды)
Как назовем точку S, не лежащую в плоскости многоугольника? (вершина пирамиды)
Есть ли еще вершины в пирамиде? (да, вершины основания)
Что еще не назвали? (отрезки, соединяющие вершину многогранника и вершины основания)
Как называются эти элементы? (боковые ребра)
Есть ли еще ребра у пирамиды? (да, ребра основания)
Какие еще элементы есть у пирамиды? Что образуют боковые ребра? (боковые грани)
Какие фигуры являются боковыми гранями любой пирамиды? (треугольники)
Есть ли еще грани? (да, это основание)
Итак, мы выделили следующие элементы пирамиды; запишем их в тетрадь
(слайд 25 до высоты): основание, грани, ребра, вершины.
Какие еще элементы мы рассматривали у призмы? (высоту)
Запишем к элементам слово – высота.. Какой буквой она обозначается? (слайд 25)
Как найти высоту в пирамиде? (расстояние от вершины пирамиды до плоскости основания).
Задание: «Проверь себя». Перед вами чертеж пирамиды. Укажите ее основные элементы. Перечерчивать не нужно. Запись сделайте в тетради. (слайд 26)
Проверка (слайд 26)
С определением и элементами пирамиды мы разобрались вместе. Теперь вам предстоит применить эти знания на практике и самим определить виды пирамиды.
практическая работа в группах по моделированию пирамид с помощью пластилина и палочек и проверка результатов работы (выступление представителей группы)
Каждая группа получает практическое задание: 1 часть работы – смоделировать призму из подручного материала по заданному условию (модель собираете на картоне из палочек, которые соединяете между собой с помощью пластилина); 2 часть – ответить с помощью полученной модели на поставленные вопросы; 3 часть – рассказать о результатах другим группам (Карточки). На работу 5 минут.
Выступление групп.
Вывод: какие же виды пирамид можно выделить?
знакомство с видами пирамид и алгоритмом построения чертежей пирамид этих видов;
Благодаря своим предыдущим знаниям и смекалке вы получили следующие виды пирамиды: n- угольную, прямую и наклонную. К сожалению ни того, ни другого вида пирамид в математике не выделяют, хотя вы однозначно правы.
При определении вида пирамид математики обратили внимание на 2 вещи: длины сторон основания и куда проецируется высота. Т. о. пирамиды предложено делить на следующие виды:
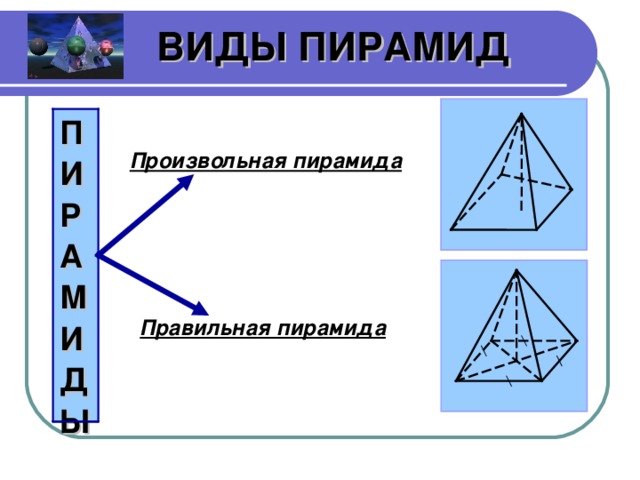
правильная и произвольная (слайд 27).
Как вы думаете, какая из смоделированных вами пирамид будет правильной?Почему?
Запишем определение правильной пирамиды. (слайд 28 - определение)
Правильная пирамида – это пирамида, в основании которой лежит правильный n-угольник и основание высоты является центром основания многогранника.
Все остальные пирамиды называются произвольными.
Построим правильную пирамиду. Обратите внимание на такой нюанс: четное или нечетное количество сторон у нашего многоугольника. Поэтому сделаем 2 чертежа: для четного количества сторон на примере 4-х угольной пирамиды, а для нечетного – на примере треугольной пирамиды.
С чего начнем построение. (изобразим правильный n-угольник).
Как называется правильный четырехугольник (квадрат). Чертим квадрат под углом.
Как называется правильный треугольник (равносторонний). Чертим треугольник под углом.
Теперь надо найти центры этих многоугольников. Для этого в многоугольниках с четным количеством сторон проводим диагонали и находим точку их пересечения.
В многоугольниках с нечетным количеством сторон проводим медианы. Что такое медианы? Находим точку их пересечения. Достаточно двух медиан и двух диагоналей.
Из точки пересечения поднимаем высоту произвольной длины, в зависимости от условия задачи. Определяем вершину пирамиды.
Проводим отрезки, соединяем вершину пирамиды и вершины основания. Обозначаем.
А в каком порядке будет строиться произвольная пирамида? Надо находить центр? В какой точке должно находится основание высоты? Да основание высоты может быть в любой точке, если в задаче нет на этот счет никаких указаний.
В правильной пирамиде существует еще один элемент, не названный ранее (слайд 28 - апофема). Запишите определение и построим ее.
На какой грани нужно изображать апофему? Проверим, действительно ли на любой. Мы переходим к свойствам правильных пирамид.
формулирование свойств правильных пирамид;
Если внимательно рассмотреть модели правильных пирамид можно выделить несколько их особенностей, которые являются свойствами правильных пирамид. (слайд 29).
На столах у каждой группы находится модель правильной пирамиды. Возьмите линейки и измерьте:
длины боковых ребер в каждой пирамиде. Что можно сказать об этой величине?
Какой вывод можно сделать? Из чего состоят боковые грани ваших пирамид? Какие это треугольники?
Что можно сказать о длинах апофем ваших пирамид? Как правильно их измерить? Где именно будет находиться основание апофемы?
Какие же особенности у правильной пирамиды? Перечислите их. Зафиксируем их в тетрадь, как свойства правильной пирамиды (слайд 29).
вывод формул для вычисления площадей полной и боковой поверхностей;
Мы подробно разобрали элементы пирамиды, виды и свойства.
Как вы думаете, что еще нужно рассмотреть, изучая пирамиду, чтобы решать задачи?
Правильно, нам необходимы формулы для вычисления площадей полной и боковой поверхности.
Из чего складывается площадь полной поверхности пирамиды? Посмотрите на развертку .
Как записать формулу? (слайд 30)Sп. п.= Sосн.+Sб.п)
Как найти площадь боковой поверхности? Из чего складывается боковая поверхность любой призмы?
Значит, чтобы найти площадь боковой поверхности, нужно сложить площади всех боковых граней.
Как записать формулу? Sб. п. = �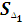 �+�
�+�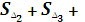 �…. +�
�…. +�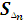 �
�
Что можно сказать о боковой поверхности правильной пирамиды? Значит формулу для вычисления боковой поверхности праавильной пирамиды можно записать в виде:
: Sб. п. прав. пирам = p�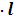 �
�
В правильной пирамиде боковая поверхность равна произведению полупериметра основания на апофему
Теоретического материала на сегодня достаточно. Попробуем применить его на практике.
Первичное закрепление - решение простых задач
Устные задачи на внимательность
Может ли пирамида иметь:
9 вершин;
16 вершин?
Существует ли пирамида, которая имеет:
20 ребер;
21 ребро?
Какой многоугольник лежит в основании пирамиды, которая имеет 32 ребра?
Определите вид пирамиды, которая имеет:
6 вершин;
22 ребра;
10 граней.
Высота пирамиды равна 3 см. Чему равно расстояние от вершины пирамиды до плоскости основания?
Боковые ребра пирамиды равны 7 см, 12 см, 5 см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?
Задачи для решения в тетради
Задача№1
В треугольной пирамиде стороны основания 7см. Расстояние от вершины пирамиды до стороны основания 11 см. Найдите площадь полной поверхности пирамиды.
Задача №2
В правильной четырехугольной пирамиде сторона основания 10 см, а высота 13 см. Найдите площадь полной поверхности призмы.
Задача №3
Основание пирамиды – ромб с диагоналями 10см и 18 см. Высота пирамиды равна проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13 см. Найдите большее боковое ребро пирамиды.
Задача №4
Основание пирамиды – прямоугольник со сторонами 6см и 8 см. Высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.
Решение задач проводится у доски и в тетради. Решение задач у доски осуществляют студенты в следующему порядке: чертеж; Дано; Найти; составляется краткий план решения и записывается на доске.
Решение задачи записывается самостоятельно по составленному плану у доски и в тетради. Затем решения сравниваются.
6. Домашнее задание:
Сторона основания правильной четырехугольной пирамиды равна 12 см. Расстояние от вершины пирамиды до стороны основания 10 см. Найдите площадь полной поверхности пирамиды.
7. Итог урока
С каким новым многогранником вы познакомились?
1) заполните 2 столбец, аналогично первому, а в третьем напишите, чему научились
2) Закончите мои предложения:
Пирамида – это многогранник, состоящий из…
Элементы пирамиды – это…
Боковыми гранями любой пирамиды являются…
Перпендикуляр из вершины на плоскость основания – это…
Перпендикуляр из вершины на сторону основания – это…
Пирамиды бывают 2-х видов:…
Чтобы построить правильную пирамиду нужно высоту установить…
Площадь полной поверхности пирамиды вычисляется по формуле:…
Боковая поверхность правильной пирамиды равна произведению…