Представленный урок является повторительно-обобщающим по теме "Производная.Геометрический и механический смысл производной" и позволяет повторить тему "Производная", применение производной для нахождения угла наклона касательной к графику функции, значение производной в указанной точке и позволяет составлять уравнение касательной к графику функции, проходящей через точку х. Также повторяются основные функции и их графики, производные и их графики. При повторении механического смысла производной предлагаемые задачи позволяют находить скорость движущейся точки, если известно изменение координаты и ускорение в какой-то момент времени.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Урок"Производная. Геометрический и механический смысл производной"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок"Производная. Геометрический и механический смысл производной" »
Полезное для учителя
Распродажа видеоуроков!
1750 руб.
2500 руб.
1670 руб.
2380 руб.
1460 руб.
2090 руб.
1670 руб.
2380 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




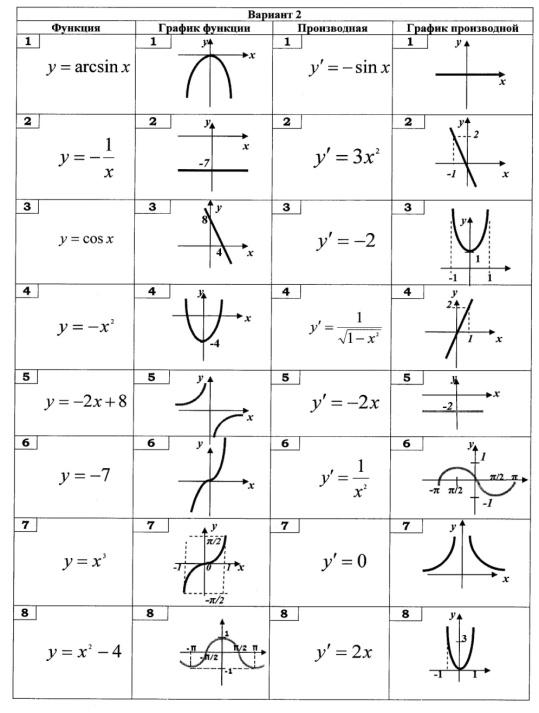
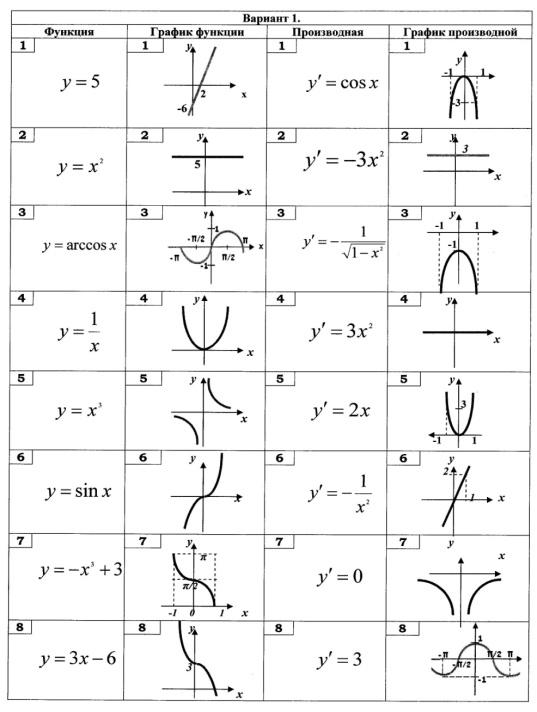
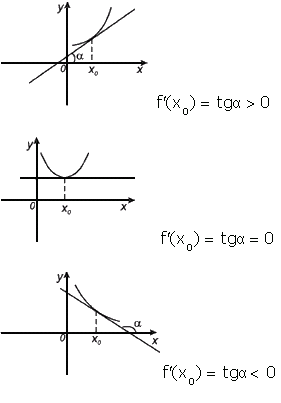

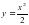 в точке с абсциссой х
в точке с абсциссой х =8
=8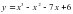 в точке М
в точке М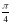 2)
2)  3)
3)  4)
4)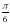
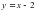 касается графика функции
касается графика функции 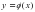 в точке
в точке 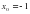 .Найдите
.Найдите 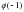 .
.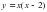 в точке с абсциссой
в точке с абсциссой 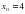 .
.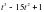 . В какой момент времени ускорение будет равно нулю?
. В какой момент времени ускорение будет равно нулю?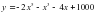 ?
?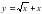 в точке с абсциссой
в точке с абсциссой 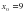
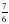 2)
2) 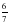 3)
3) 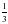 4) 3
4) 3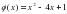 . Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.
. Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.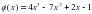 в точке с положительной абсциссой
в точке с положительной абсциссой 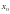 ,равен 2. Найдите
,равен 2. Найдите 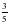 2) 0 3)
2) 0 3) 



















