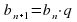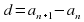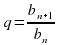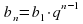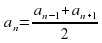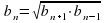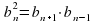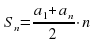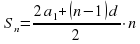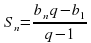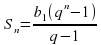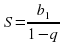Тема урока «Сумма n первых членов геометрической прогрессии».
Тип урока - урок изучения и первичного закрепления новых знаний.
Образовательные цели:
- построение знаний о сумме n-первых членов геометрической прогрессии, самостоятельное выведение формулы для нахождения n-го члена геометрической прогрессии;
- развитие исследовательских умений анализировать и синтезировать информацию;
- осознание практической значимости полученных знаний.
Воспитательные цели:
- воспитывать самостоятельность, аккуратность при решении задач, а также умение самостоятельно добывать знания;
- содействовать формированию мировоззренческих понятий;
- формирование эмоционально- личностной сферы учащихся
- формировать умение высказывать свою точку зрения; доказывать свою правоту; признавать свои ошибки и правоту одноклассников.
Развивающие цели:
- развивать логическое мышление, математическую речь,
- учить записывать информацию кратко на математическом языке,
- Развивать познавательные интересы у учащихся и их умения применять знания по математике к решению жизненных задач.
Ход урока.
- Организация начала урока.
- Проверка домашнего задания.
- Устная работа. Актуализация знаний учащихся
- Какая из последовательностей является геометрической:
- 2,3; -3,5; 4,7; -5,9; …;
- -½; 1; -2; 4;…;
- 3; 9; 27; 81;…;
- 3; 5; 7; 9;…? Есть ли здесь арифметическая прогрессия?
- Является ли число членом геометрической прогрессии 8; 4; 2;…?
Если является, то укажите его номер.
Ответ: да, n = 6.
3. Изучение новой темы.
Итак, просьба мудрого Сеты помогла Вам понять определение геометрической прогрессии, и теперь настало время узнать что-же было дальше…. За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли Сета свою жалкую награду.
-Повелитель, - был ответ, - приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
-Повелитель, - ответили ему, - математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение.
Царь приказал ввести его.
-Прежде чем скажешь о твоем деле, - объявил Шерам, - я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
-Ради этого я и осмелился явиться перед тобой в столь ранний час, - ответил старик. – Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико….
-Как бы велико оно ни было, - надменно перебил царь, - житницы мои не оскудеют. Награда обещана и должна быть выдана.
- Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, которое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни.
Пусть все пространство их будет сплошь засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду… С изумлением внимал царь словам старца.
- Назови мне это чудовищное число, сказал он в раздумьи.
18 446 744 073 709 551 615
-Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!
- Награда шахматного изобретателя должна была бы занять 12 000км3.
- При высоте амбара 4м, ширине 10м, его длина должна была бы быть 300 000 000 км, - что вдвое дальше, чем от Земли до Солнца!
Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, - но что награда, о которой говорит предание, должна была выразиться именно таким числом в этом ты сам можешь убедиться.
Фактически, число зерен, о которых идет речь, является суммой 64 членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
S = 1+2+22+23+24+…….+262+263
Умножим обе части записанного равенства на знаменатель прогрессии 2, получим:
2S = 2+22+23+24+ ……….+264
Вычтем почленно из второго равенства первое и проведем упрощения: 2S – S = ( 2+22+23+24+….+264) – (1+2+22+23+24+……+263)
S = 264 - 1
S = 264 – 1
Значит, подсчет зерен сводится к перемножению 64 двоек. Для облегчения выкладок заменим 264 = (210)6 · 24 =
=1024 · 1024 ·1024· 1024 ·1024· 1024· 16 =
=1048576 ·1048576 ·1048576 ·16 – 1
и получим искомое число зерен:
18 446 744 073 709 551 615
Масса такого числа зерен больше триллиона тонн.
Индусский царь не в состоянии был выдать подобной награды.
Но будь он силен в математике, он бы не попал впросак…
Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии.
Воспользуемся тем же приемом, с помощью которого была вычислена сумма зерен.
Пусть дана геометрическая прогрессия (bn). Обозначим сумму n первых ее членов через Sn:
Sn = b1 + b2 + b3 +………+bn-1 + bn. (1)
Умножим обе части этого равенства на q: Sn ·q = b1· q + b2 ·q + d3· q +….+bn· q
Учитывая, что b1· q = b2, b2· q = b3,……bn-1· q = bn,
получим: Sn·q = b2 + b3 + b4+ ……+bn + dn· q (2)
Вычтем почленно из (2) равенство (1) и приведем подобные члены : Sn·q – Sn = (b2+b3+b4+….+bn+bn·q) – (b1+b2+b3+….+bn) = bn·q – b1 Þ Sn(q – 1) = bn·q – b1
Sn = (bn·q – b1) / (q – 1)
Таблица: "Арифметическая и геометрическая прогрессии".
Арифметическая прогрессия
Геометрическая прогрессия
Примеры
1;5;9;13;.
1;2;4;8;18…
Определение
an+1 = an + d
Разность / Знаменатель прогрессии
Формула n-го члена аn = а1 + (n – 1) d
Свойство
Формула суммы n первых членов.
4. Практическое применение нового материала.
Решение упражнений № 776(в,г),779(б),781(б),782(а-г)
5. Подведение итогов урока. Рефлексия.
6. Домашнее задание. П.19. № 776(а,б),779(а),781(а)
7. Заключительный этап урока.