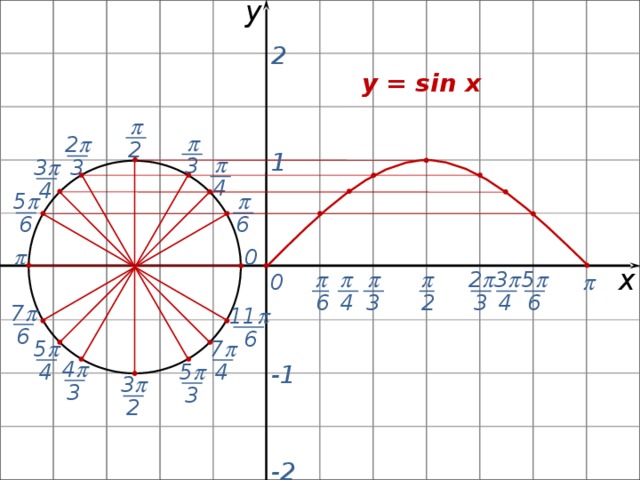
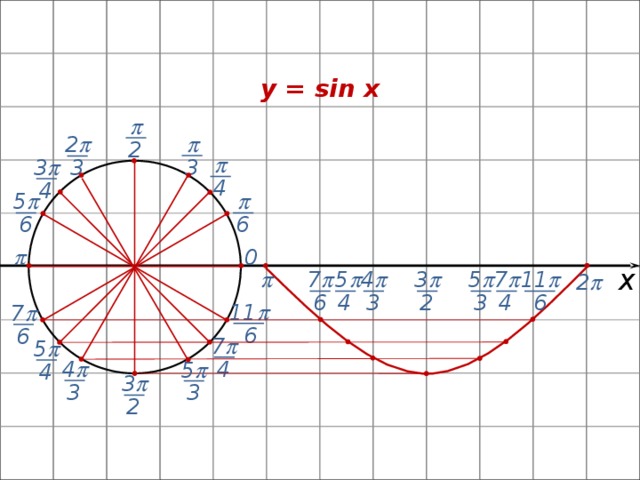
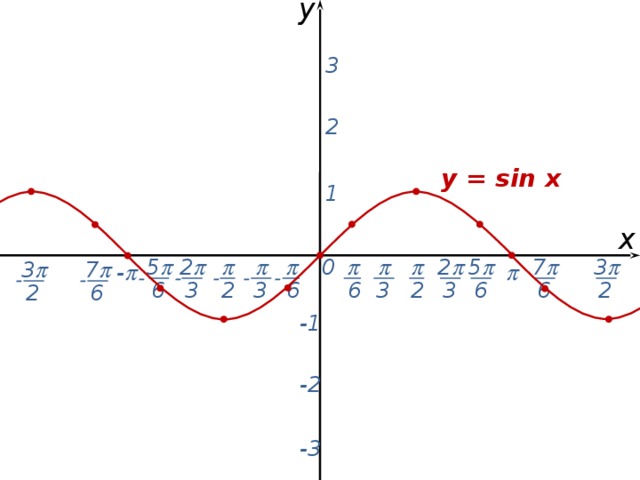
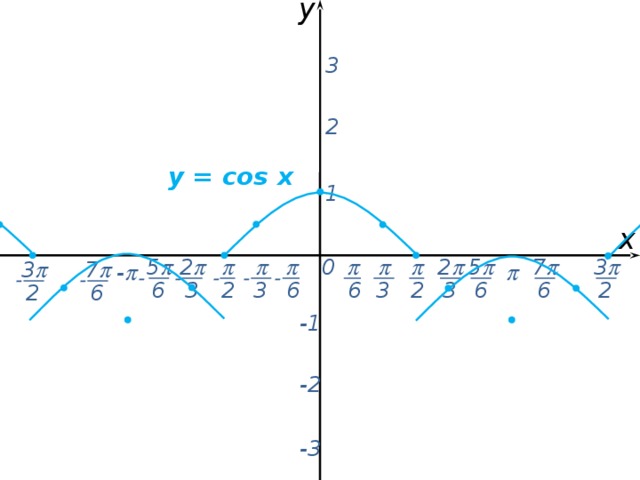
Из истории тригонометрии. Леонард Эйлер - крупнейший математик 18-го столетия. Родился в Швейцарии. Долгие годы жил и работал в России, член Петербургской академии. Почему же мы должны знать и помнить этого учёного?
К началу 18 века тригонометрия была ещё недостаточно разработана: не было условных обозначений, формулы записывались словами, усваивать их было трудно, неясным был и вопрос о знаках тригонометрических функций в разных четвертях круга, под аргументом тригонометрической функции понимали только углы или дуги. Только в трудах Эйлера тригонометрия получила современный вид.